Beddoes Method
Another method, originally devised by Beddoes (1983), uses the Kirchhoff or Helmholtz solution for the lift on a flat-plate with a fixed separation point to model the
 |
|
nonlinear airfoil characteristics. In the Kirchhoff-Helmholtz model, the lift or normal force coefficient on the airfoil, Cn, is approximated by the equation
where 2tt is the normal force-curve-slope for incompressible flow, / is the trailing edge separation point (nondimensionalized with respect to chord), and a is the AoA – see Thwaites
(1960) . Thus, if the separation point can be determined (the difficult part), it is easy to compute the normal force coefficient. The expression in Eq. 7.104 may also be extended to encompass compressible flows where In is replaced by the force-curve-slope at the appropriate Reynolds number and Mach number [i. e., Cna{Re, Moo)], and a is measured relative to the zero lift angle, that is,
C„=C„JRe. Mt>0)(l+^7 (a-oro). (7.105)
To practically implement this procedure, the relationship between the separation point, /, and the AoA, a, must be obtained. These data are not generally known; however, an “effective” trailing edge separation point, /, can be deduced from the experimental measurements of the static Cn variation with a by rearranging Eq. 7.105 to solve directly for f, that is,
/ = I 2 /———- ————- 11 . (7.106)
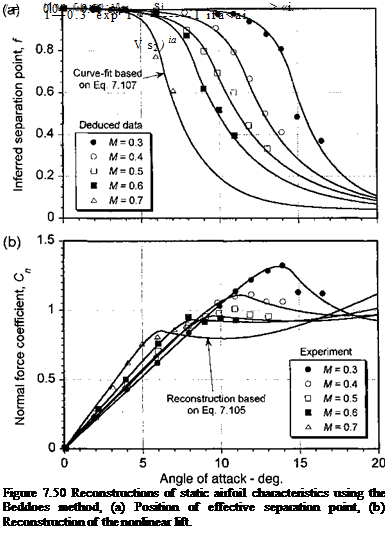
The resulting curves are given by Beddoes (1983) and have been recalculated in Fig. 7.50 for the NACA 0012 airfoil over a range of Mach numbers.
After the values of / have been found, the lift at any AoA can be found by interpolating the values of / and finding the corresponding nonlinear value of C„ using Eq. 7.105. Beddoes (1983) shows that the,/ versus a curves all have a characteristic shape for all
 |
|
Mach numbers, which turns out to be extremely convenient because the variations can then be generalized empirically in a fairly simple manner using the curve fits
The coefficients Si and S2 define the static stall characteristic, that is, whether the stall occurs progressively or abruptly. The value of a defines the break point corresponding to f — 0.1. This point is defined only as a matter of convenience; however, the value of a when / ~ 0.7 closely corresponds to the static stall AoA. The coefficients Si and S2 and a are easily determined for different Mach numbers from the static lift data. Their values are read from a data table, with values for intermediate Mach numbers being performed using interpolation, as required – see Beddoes (1983).
The pitching moment as a function of AoA can also be found from Kirchhoff-Helmholtz theory. However, in practice the resulting equation is found inadequate and Beddoes has suggested several empirical relations. From the airfoil static data, the center of pressure at any AoA may be determined from the ratio CmfCn (allowing for the zero lift moment CWo). The variation can be plotted versus the corresponding value of the separation point and curve fitted using a low-order polynomial. One suitable curve fit is to use the form
-^=ко + т~/) + к2$т(2тгГ), (7.108)
where ко = (0.25 — xac) is the aerodynamic center offset from the 1 /4-chord. The constant k gives the direct effect on the center of pressure as a result of the growth of the separated flow region, and the constant &2 helps describe the shape of the moment break at stall. Again, the values of ко, k, ki, and m can be obtained using a least-squares fit to the measured center of pressure.











