C. G. LIMITS
One of the dominant parameters of longitudinal stability and control has been shown in Chapter 6 to be the fore-and-aft location of the C. G. The question now arises as to what range of C. G. position is consistent with satisfactory flying qualities. This is a critical design problem, and one of the most important aims of stability and control analysis is to provide the answer to it. Since aircraft always carry some disposable load (e. g. fuel, armaments), and since they are not always loaded identically to begin with (variations in passenger and cargo load), it is always necessary to cater for a variation in the C. G. position. The range to be provided for is kept to a minimum by proper location of the items of variable load, but still it often becomes a difficult matter to keep the flying qualities acceptable over the whole C. G. range. Sometimes the problem is not solved, and the airplane is subjected to restrictions on the fore-and-aft distribution of its variable load when operating at part load.
THE AFT LIMIT
The most rearward allowable location of the C. G. is determined by considerations of longitudinal stability and control sensitivity. The behavior of
|
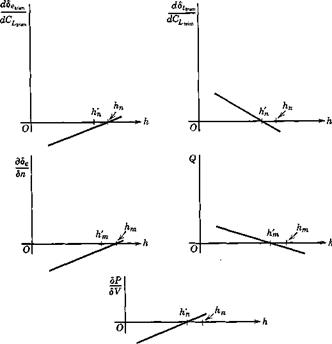
Fig. 7.10 The five control gradients. |
the five principal gradients discussed in Chapter 6 are summarized in Fig.
7.10 for the case when the aerodynamic coefficients are independent of speed. From the handling qualities point of view, none of the gradients should he “reversed,” i. e. they should have the signs associated with low values of h. When the controls are reversible, this requires that h < h’n. If the controls are irreversible, and if the artificial feel system is suitably designed, then the control force gradient dP/dV can be kept negative to values of A > h’n, and the rear limit can be somewhat farther back than with reversible controls. The magnitudes of the gradients are also important. If they are allowed to fall to very small values the vehicle will be too sensitive to the controls. When the coefficients do not depend on speed, as assumed for Fig. 7.10, the N. P. also gives the stability boundary (this is proved in Chapter 9), the vehicle becoming unstable for h> h’n with free controls or h > hn with fixed controls. If the coefficients are not independent of speed, e. g. Gm = Cm( M), then the C. G. boundary for stability will be different and may be forward of the N. P. However (this is also shown in Chapter 9) the
nature of the instability is very much dependent on whether C is greater or less than zero, i. e. on whether the C. G. is forward or aft of the relevant N. P. In the former case the instability is less severe than in the latter, and hence the N. P. still provides a good practical criterion for stability.
By the use of automatic control systems (see Chapter 11) it is possible to increase the natural stability of a flight vehicle. Stability augmentation systems (SAS) are in widespread use on a variety of airplanes and rotorcraft. If such a system is added to the longitudinal controls of an airplane, it permits the use of more rearward C. G. positions than otherwise, but the risk of failure must be reckoned with, for then the airplane is reduced to its “natural” stabihty, and would still need to be manageable by a human pilot.