CHECKING A SMALL GAIN CONDITION DESPITE MODEL UNCERTAINTIES
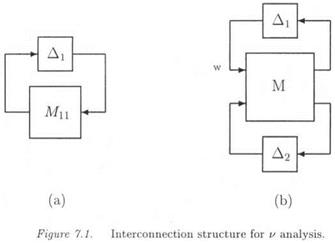
• Let the interconnection structure Ми— Ді of Figure 7.1.a, in which the full complex block Ді represents either a block of neglected dynamics, or a fictitious performance block (see section 4.4 of chapter 1). Мц contains the closed loop dynamics and the weighting function, the latter corresponding either to the template on the neglected dynamics, or to the performance requirement (i. e. the template on the closed loop transfer matrix of interest). In the rest of the subsection, the complex matrix Mi i typically represents the value of the transfer matrix Mn(s) at s = ju> (the same remark can be applied to the complex matrices M and Мц).
On the one hand, if A represents a block of neglected dynamics, this one is assumed to be maintained inside its unit ball (i. e. ст(Ді) < 1). The small gain theorem gives then a condition of stability of the interconnection structure, namely:
![]() ct(Mu) < 1
ct(Mu) < 1
 |
On the other hand, if Ді represents a fictitious performance block, nominal performance is achieved if equation (7.1) is satisfied.
The transfer Fi(M, A2) between w and z (with Ді = 0 on Figure 7.1.b) can be computed as:
![]() Fi(M, Д2) = Mu + Мі2Дг(/ — М22Д2) [8]Мгі
Fi(M, Д2) = Mu + Мі2Дг(/ — М22Д2) [8]Мгі
If W 1 represents a block of neglected dynamics which is to be maintained inside its unit ball, the small gain theorem gives then a condition of stability of the interconnection structure of Figure 7.1.b, namely ‘:
![]() a(Ft(M, Д2))<1
a(Ft(M, Д2))<1
On the other hand, if Ді represents a fictitious performance block, robust performance (in the face of the model perturbation W2 ) is achieved if equation (7.4) is satisfied.
The issue is to find the maximal size of the structured model perturbation Д2 which still satisfies, either the robust stability property in the presence of a given amount of neglected dynamics Ді, or the robust performance property (if Ді is a performance block). This maximal size is given by l/i>(M):
v(M) = l/min(k / ЭД2 Є кВА2 with M = Fi(M, Д2) anda(M) > 1)











