Coherent structures as a sound source

We now turn our attention to the mechanisms by which such coherent structures may be active as sound sources. We will work in the context of Lighthill’s acoustic analogy, whence by means of theoretical considerations it will be possible to gain some insight regarding pertinent simplifications. We are, therefore, in what follows, working in the context of steps 3, 4 and 5 of the analysis methodology outlined earlier; and with regard to the filtering operation, FqA, we are in context (iii).

The wavepacket source ansatz Mollo-Christensen (1967) appears to have been first to propose a mechanism by which coherent structures might be active as a source of sound. Observing that the nearfield pressure sig­nature of the subsonic jet presents a surprising degree of organisation in the (yi, t) plane, he suggested that such organisation could result in the jet behaving as a ‘semi-infinite antenna for sound’. Where this kind of sound production is concerned, a convected wavepacket constitutes a pertinent model for the organised component of the flow. Such a model, first ex­plored by Michalke (1971) and Crow (1972), continues to be widely used by researchers today, even if there is probably some disagreement with regard to the salient sound-producing features and dynamic law of such wavepack – ets.

Our presentation of the wavepacket sound source is organised as follows:

• We begin by introducing the basic wavepacket source ansatz, as pro­posed by Michalke (1971), Crow (1972) (see also Crighton (1975)),

• We then outline some of the arguments used to justify its simple line – source form: the elimination of the radial dimension is a good example of observable-based simplification,

• We next present a comparison of experimentally obtained acoustic data with the sound field characteristics of the wavepacket model,

• We then discuss, in greater detail, the radiation mechanism associated with wavepackets, exploring a number of different kinds of behaviour which lead to its being enhanced:

1. Spatial modulation,

2. Temporal modulation,

3. Temporally-localised wavepacket truncation,

4. Space-time ‘jitter’.

• Finally, we present, in section §4, two case studies, in which a num­ber of numerical databases (obtained both by Large Eddy Simula­tion and by Direct Numerical Simulation) are analysed, following the methodology outlined earlier, and the salient sound-producing fea­tures of wavepackets thereby educed.

The basic wavepacket model First attempts to explore the wavepacket ansatz as a kinematic model for the organised component of the jet were made by Michalke (1971), Crow (1972) (see also Crighton (1975)). The physical problem considered is that of small amplitude acoustic disturbances propagating through a quiescent, homogeneous medium, as a result of an externally-imposed source term:

9 p(x t) -^p(x, t) = s(y, t), (71)

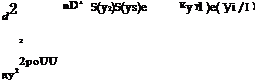where the source takes the following form:

The solution of the spherical wave equation to an externally-imposed exci­tation of this kind is:

where Mc is the Mach number based on the phase velocity of the convected wave, Uc.

As outlined in section §2, equation 73 results from a convolution of the source ansatz with the free-space Green’s function, this operation identify­ing the source characteristics to which the radiated sound field is sensitive.

One of these characteristics, visible in the solution, is the source compact­ness, kL. Figure 5 shows how for small values of kL the source is com­pact, while for larger values it becomes non-compact, exhibiting numerous oscillations over its spatial extent. The corresponding dependence of the sound field directivity is shown in the right-hand figure: the less compact the source, the more the sound field is ‘beamed’, due to an antenna ef­fect, to shallow axial angles. For kL = 6 the directivity pattern is close to exponential; sources exhibiting such exponential directivity are termed superdirective (Crighton and Huerre (1990)).

It can be seen in equation 72 that the source is concentrated on a line (by 5(y2)5(y3)). This may seem strange considering that the turbulent re­gion of a propulsive jet fills a volume that is approximately bounded by a conical surface. This simplification can be justified, however, by appeal­ing to the radiation efficiency of different azimuthal modes of a cylindrical source (which is a slightly better approximation to the real dimensions of a jet, particularly when one considers the regions of maximal turbulence intensity: these lie on such a cylindrical surface). In the following section we outline this justification; this is an exercise in system reduction based purely on theoretical arguments: we use the Lighthill acoustic analogy for­mulation to demonstrate how certain ‘directions’ of the source system can be disregarded: the conclusion that we come to is that equation 72 is a rea­sonable approximation for the coherent structures where low-angle sound emission is concerned.

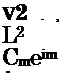Radiation efficiency of azimuthal modes The following is taken from Cavalieri et al. (2010b) and Cavalieri et al. (2011a), similar analysis being found in Michalke (1970). Consider a source term of the form

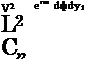Where m denotes azimuthal Fourier mode number, and Cm the correspond­ing Fourier coefficient. The corresponding solution of the wave equation can be written

We assume, without loss of generality, that the observer is at Ф = 0 and x2 = 0 in cartesian coordinates, where Ф = tan-1(x2/x3). The distance can be expressed, with a far-field assumption, as,

p(x, t) = poUUR2 d2 4nc2|x| dt2

where в is the angle of x to the jet axis. The solution thus becomes

p(x, t) = poUuR2 d2 Г“ 4nc2|x| dt2 J_c

p2n I1 = e1(mф)e(_1пStM cos ф s1n в)(ц 0

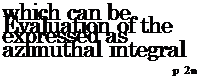which can be rearranged as

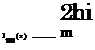indicates the radiation efficiency of azimuthal mode m; i. e. the capacity of that azimuthal source mode to couple with the acoustic field.[13] This integral can be expressed in terms of Bessel functions Jm,

giving

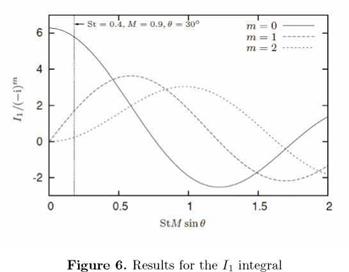
I1 = (-i)m 2nJm(nStM sin в). (82)

For StM sin в = 0 the I1 integral yields 2n for m = 0, and 0 for all other values of m. This means that, if we neglect retarded time differences along the azimuthal direction, which is justified if this direction is acoustically compact (i. e., the acoustic wavelength is much larger than the azimuthal wavenumber, which being always smaller than the jet diameter, D, allows

the compactness criterion to be expressed in terms of the jet diameter: D/X = StM) only axisymmetric wave-packets can radiate. In other words, if the wave-packet diameter D is compact, or, if the observation angle в is small, only the axisymmetric wave-packet has significant radiation. This is always true for в = 0 and в = n, i. e. for an observer on the jet axis (Michalke (1970); Michalke and Fuchs (1975); Michel (2009)).

Figure 6 shows the Ii integral, divided by (— i)m so as to yield a real quantity. We see that the integral of m = 0 decays from its compact value of 2n, eventually goes to zero, and then oscillates. The integrals for the higher azimuthal modes are zero at the compact limit, as expected from the properties of the Bessel functions; they go from zero to a certain value, which is of the same order of the m = 0 integral, and then oscillate.

In order to appreciate the implications for a realistic jet flow, consider the sound radiation to low axial angles from a high Mach number subsonic jet. Taking в = n/6, M = 0.9 and St = 0.4, we have StM sin в = 0.18, and in this case, as seen in fig. 6, we can, if we have similar amplitudes Cm for the different m values, neglect all modes m > 0 and consider the compact limit (Ii = 2n for m = 0) as a first approximation; the Ii integral for m = 1 yields a sound intensity 10dB lower than that for m = 0, the integrals for higher m modes being lower still. Suzuki and Colonius (2006) have provided experimental evidence showing that the peak amplitudes, Cm, for azimuthal modes m = 0 and m =1 are similar, the amplitudes of mode m = 2 being

somewhat lower.

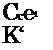If we retain only the axisymmetric wave-packet and approximate Ii as 2n, we have

and integration gives

which is the same result obtained using the line source in equations 71, 72 and 73. This means that for small values of the parameter StM sin в, the use of a wave-packet concentrated on a line leads to the same result as a surface wave-packet, justifying therefore the use of a line distribution for Til, whose amplitude is that of the azimuthal mean of the и fluctuation on the jet lipline. We will see, later, the extent to which this considerably sim­plified source model, and variants thereof, can mimic the sound-producing behaviour of a turbulent jet. In particular, we will be interested in some important additional modifications, identified thanks to the application of the analysis methodology outlined earlier, which are necessary in order that the ansatz be capable of producing quantitative agreement with the sound field radiated by the turbulent jet. First, however, let us examine some ex­perimental data, comparing, qualitatively, with the basic wavepacket ansatz outlined above.

Experimental evidence of wavepacket radiation The following re­sults are taken from Cavalieri et al. (2011b). The experiments were per­formed at the Bruit & Vent jet-noise facility of the Pprime Institute. The setup is shown in figure 7. The exit diameter of the jet is D = 0.05m, the flow is isothermal, and the exit velocity is varied over the Mach num­ber range 0.3 < M < 06; the corresponding Reynolds number range is

3.7 x 105 < Re < 5.7 x 105, and the boundary layer is tripped in all cases so as to ensure that at the outlet it is fully turbulent. Acoustic measurements are performed by means of an azimuthal distribution of six microphones at a radial distance of 35D, and the axial position of the ring array was variable. In this way the directivity of the sound field, decomposed into azimuthal Fourier modes, can be studied. These measurements can then be compared with the sound field of the wavepacket ansatz discussed above; in particular we focus on the axisymmetric component. Figure 7(b) shows the directivity in terms of both the overall SPL and the contributions from

(a) (b)

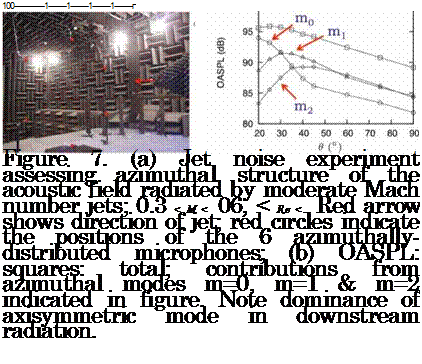
each of the first three azimuthal Fourier modes, m = 0, m =1 and m = 2. The axisymmetric component, m = 0, dominates the downstream radiation, sideline radiation comprising larger contributions from modes m = 1 and m = 2.

The dominance of the low-angle radiation by the axisymmetric mode is consistent with the foregoing analysis of the efficiency of azimuthal source modes, suggesting the existence of wavepacket radiation. By continuing to interrogate the experimental data with respect to the wavepacket model characteristics, we can evaluate the extent to which this model is pertinent.

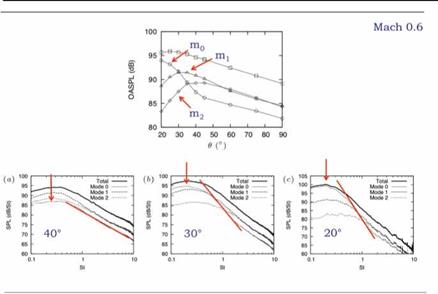
Concentrating now on the lower emission angles, assessing the power spectral density as a function of emission angle and azimuthal Fourier mode, we obtain the result shown in figure 8. As we move from 40° to 20° we observe the progressive emergence of the axisymmetric component of the power spectrum, and we note that this emergence occurs over a relatively narrow spectral range, with peak frequency StD = 0.2. The energy of the axisymmetric component of the sound field finds itself concentrated at low angles (highly directive) and across a relatively narrow range of frequency. At the lowest emission angles the peak of the overall spectrum is almost entirely axisymmetric, the energy of mode m = 0 being 10dB (that is one

Figure 8. Power spectra of azimuthal modes 0, 1 & 2 at low emission angles.

Figure 9. Narrowband-filtered (at StD = 0.2) directivity of azimuthal modes and comparison of axisymmetric mode with wavepacket ansatz. Ax – isymmetric component of experimentally obtained sound field is superdirec­tive (exponential polar decay) in agreement with the wavepacket model

Figure 10. Azimuthal mode directivities as a function of Mach num­ber. Axisymmetric mode is superdirective for all Mach numbers; indicates wavepacket radiation even at low Mach number

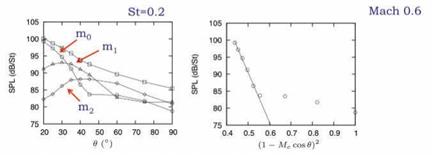
order of magnitude) greater than the next most energetic azimuthal mode, m =1. The narrowband character of the emergence of the axismmetric mode, whose energy is concentrated at StD = 0.2, justifies an assessment of the directivity of the SPL in a narrow frequency range centered at this frequency. The result is shown in figure 9(a), where the downstream direc­tivity of the axisymmetric component at this frequency is even more marked. Comparison can now be made with the directivity factor of the wavepacket ansatz, (1 — Mc cos d)2; this is done in figure 9(b). The exponential char­acter of the axisymmetric component of the sound field, when plotted as a function of this wavepacket directivity factor again suggests that the asso­ciated underlying source mechanism is associated with an axially extended wavepacket of the kind modelled by equation 72. The term superdirectivity was coined by Crighton and Huerre (1990) to describe such directivity.

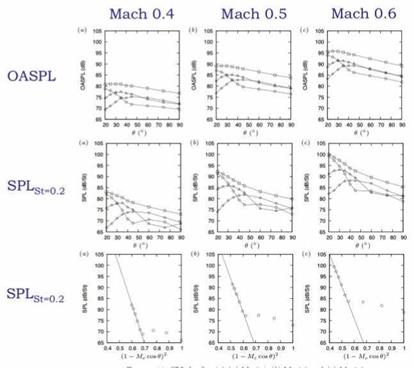
It is now of interest to study two further aspects of the experimental sound field: the Mach number dependence and the spectral scaling; both will allow further insight with regard to the possibility that the downstream radiation is underpinned by these relatively simply wavepacket source func­tions. Figure 10 shows the OASPL and narrowband-filtered SPL as a func­tion of emission angle for the different azimuthal Fourier modes of the sound field, as a function of jet Mach number. The result shows that precisely the same behaviour observed at Mach 0.6 is also observed at lower Mach number, suggesting that wavepacket radiation is a dominant mechanism for low-angle emission, even at low Mach number.

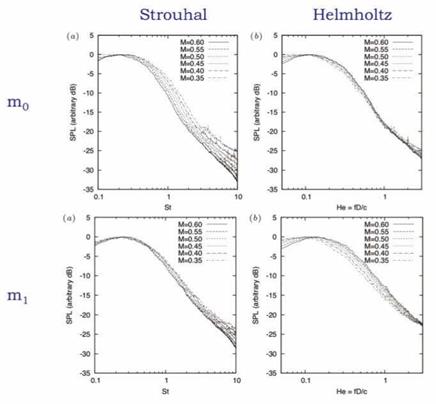
Finally, we assess the scaling of spectra for the modes m0 and mi, as a function of Mach number, for emission angle в = 30°. The result is shown in figure 11, where both Strouhal (StD = fD/Uj) and Helmholtz (He = D/X) numbers are assessed. For the axisymmetric component of the sound field we find that Helmholtz scaling best collapses the sound spectra. As the Helmholtz number is the ratio of a characteristic flow scale to a characteristic scale of the sound field, the fact that this parameter collapses the axisymmetric component of the sound field suggests that the associated source is non-compact, as it suggests that this component of the sound field is sensitive to the ratio between flow scales and acoustic scales; this would not be so for a compact source, where a clear scale separation exists between acoustic waves and flow eddies.

By comparing the experimental data with the details of the wavepacket ansatz, it is possible to make a quantitative estimate of the wavepacket compacntess parameter, kL, which can be written as

2П T

Lk = Mc HeD – (85)

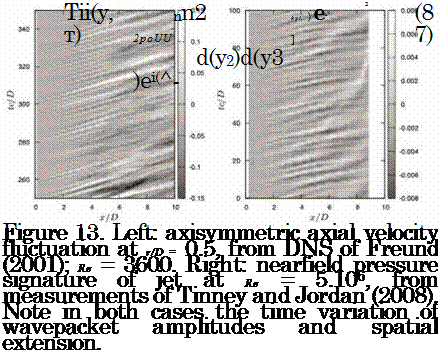
Considering the jet at M = 0.6, we have, Mc = 0.36, He = 0.12 and D = 0.05. For the same jet the directivity of the axismmetric mode is char­acterised by a decrease of 15.6dB over the angular range 20° < в < 45°, which allows us to estimate that the compactness parameter, Lk = 6.5. Comparison with figure 5, gives a sense of the corresponding wavepacket structure; this value, which suggests that the wavepacket extends over an axial region of about 6D, is consistent with the analysis of Hussain and Zaman (1981), who educed coherent structures from low Mach number tur­bulent jets by means of conditional averaging of hotwire measurements.

Figure 11. Scaling of azimuthal modes 0 and 1. Axisymmetric mode scales best with Helmholtz number, He = D/X, suggesting that it is associated with a non-compact source. Substituting the experimental parameters into the wavepacket model we can deduce that Lk = 6.5; comparison with figure5 shows that this implies wavepacket with a spatial structure com­prising about three oscillations, extended over approximately 6D, i. e. from the jet exit to beyond the end of the potential core.

The radiation mechanism Let us now consider the details of the mecha­nism by which sound sources, and in particular, ‘coherent structures’, excite acoustic modes in turbulent flows. The mechanism can be understood by considering the acoustic analogy, written down either as a partial differen­tial equation, or expressed in terms of its integral solution; time-domain, frequency-domain and linear alebrai’c formulations of both the inhomoge­neous PDE and its integral solution can be helpful in understanding the essentials: the sound production mechanism can be thought about in three different ways; we can say that:

1.Space-time inhomogeneity of the source field is such that cancellation (in time-delayed coordinates) between regions of positive and negative stresses is incomplete; the fluid medium thus finds itself subjected to compressions and rarefactions that engender a propagative energy flux,

2.The propagation operator has an acoustic response to only those com­ponents of the source field that are acoustically-matched: those that satisfy the dispersion relation ш2 = c0|^|2; in terms of the integral solution we can say that the Green’s function filters out, from the full range of source scales, only those that satisfy that dispersion relation,

3.In terms of linear algebra we can say that the propagator maps to the farfield those components of the source with which it is aligned:

L У s(q).

In the case of the wavepacket, these different scenarios can be represented schematically as in figure 12.

Let us now consider a number of different kinds of physical wavepacket behaviour that can lead to such radiation, before going on to explore data from turbulent jets. The following is taken from Cavalieri et al. (2011a) and Cavalieri et al. (2010b).

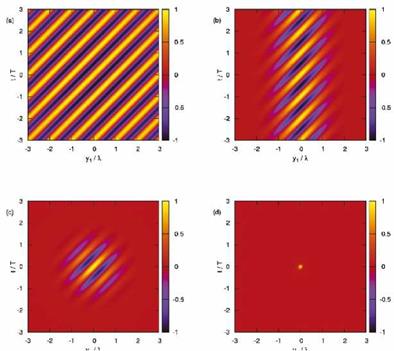
Spatial modulation The wavepacket characteristic most often referred to in the literature as important for the production of radiating sound en­ergy is its spatial modulation. A subsonically-convected spatial sinusoid of constant amplitude and infinite spatial extent contains only non-radiating scales, because ш < kxc. However, any truncation or spatial modulation of the amplitude of that wavepacket will cause its axial wavenumber spectrum to broaden, and in this way some of the wavepacket energy will find itself in the acoustically-matched region of the spectrum. Figure 12 illustrates this: (a) shows non-radiating and radiating space-time structures; (b) shows the frequency-wavenumber spectrum of a radiating wavepacket—the tail of the spectrum that finds itself in the radiating sector causes sound radiation.

Temporal modulation A further feature of the unsteadiness associated with the orderly part of a turbulent jet is its intermittency. The earlier cita­tions from Mollo-Christensen recognise this. A further citation from Crow

(c)

Figure 12. Different ways of thinking about the wavepacket radiation mechanism: (a) Space-time representation: amplitude inhomogeneities lead to incomplete cancellation, and associated compressions and rarefactions; (b) frequency-wavenumber representation; mechanism can be thought of as a filter that only passes the source components that satisfy ш2 = c^l^l2; (c) Representation in terms of linear algebra: mapping to the farfield of source by propagation operator: directions of the source, s(q), that are parallel to the propagator, L, get mapped to the farfield.

and Champagne (1971) is also relevant; they observed, by means of flow visualisation, the appearance of a train of coherent ‘puffs’ of turbulence. These were characterised by an average Strouhal number of 0.3, but the authors noted how “three or four puffs form and induct themselves down­stream, an interval of confused flow ensues, several more puffs form, and so on”.

The effect of such intermittency can considered in a number of ways. Ffowcs Williams and Kempton (1978) were the first to consider a kinematic model for such behaviour; this took the form of a random variation of the phase velocity of the convected wavepacket, as shown in equation 86. In this case the wave envelope remains time-invariant.

changes in time, as does the position where it breaks down. A model for the former effect is

Examples of this kind of space and time modulation are shown in figure 14 and this leads to a radiated sound pressure:

Figure 14. Space – and time-modulated wavepackets.

with

(90)

f (yi

where c is the speed of sound in the undisturbed fluid and в is the angle of x to the jet axis.

Evaluation of the integral of equation 90 leads to an analytical expression for the pressure in the far field:

which, after substitution in eq. (91), leads, as expected, to the earlier result for a purely spatially modulated wavepacket,

p(x, t) = — P0UuMc(kD)2Wncos2 вe-L2k2(1-Mc8)2 eiw(t-X), (98)

where Mc is the convective Mach number given by w/(kc).

We can define a source efficiency as the ratio between the acoustic energy,

the far field, and the turbulent kinetic energy, or “source” energy, given by

This allows an evaluation of the impact of changes in the space and time scales of the wavepacket envelope on the acoustic efficiency. Figure 15 shows this dependence. Note that the colour scale is logarithmic: at high Mach number small reductions in either the spatial or temporal extent of the wavepacket can lead to considerably enhanced radiation efficiency; the space-time localisation of a wavepacket is thus an important source param­eter: such behaviour in a jet comprises a flow ‘direction’ to which the wave operator is highly sensitive.

Figure 15. Wavepacket efficiency, as a function of space – and time-envelope scales, for different Mach numbers.

Temporally-localised envelope truncation In order to provide tem­poral changes in the spatial extent of the envelope function, in an effort to better model the wavepacket characteristics observed in figure 13, we can model Tii as

With this expression the peak amplitude of the convected wave is kept constant, but the characteristic length of the envelope, L, changes with time. We model the changes in L as

-t0)2

L(t ) = L0 — кє TL, (102)

where L0 is an initial envelope width and к is the maximum envelope reduc­tion, which happens at t = t0. This reduction of the envelope occurs over an interval characterised by the temporal scale tl, and is modelled by a Gaussian function. Examples of this source behaviour are shown in fig. 16. The sound radiation is obtained in this case by numerical integration using this line source. A sample result is shown in figure 16: we note that the envelope truncation also leads to an enhancement of the sound radiation, again suggesting that this kind of unsteadiness, observed in the numerical and experimental data, may underpin the emission of high-amplitude acous­tic perturbations to the far field of turbulent jets: again, in the spirit of the system reduction at the heart of the analysis methodology evoked earlier,

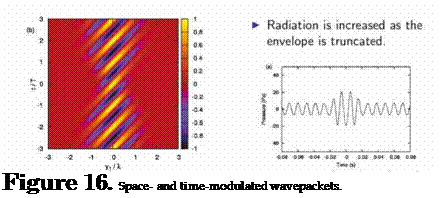the propagation operator is sensitive to this kind of flow behaviour, and so such flow ‘directions’ should, again, be retained, i. e. explicitly modelled.

We now consider a final model, which takes us closer again to the be­haviour we observe in the data shown in figure 13. We wish to mimic the space-time ‘jitter’ manifest in the data, we must therefore capture the time variation of the wavepacket envelope in terms of both its peak amplitude and its axial extent. This final model combines the effects modelled individually in the two previous models.

Space-time ‘jitter’ Tii is now modelled as

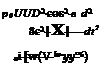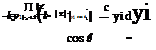where we allow temporal variations of the amplitude Л, and also tempo­ral changes in L. This expression, used in conjunction with the far-field assumption, leads to:

If the amplitude Л and the characteristic length of the envelope, L, change slowly when evaluated at retarded-time differences (y1 cos в/c) along

the wave-packet, we can consider axial compactness for these functions in the integration, such thatConclusion

In this section we have considered the source modelling problem from the perspective of ‘coherent structures’. It has been shown how consider­able simplifications can be justified where the associated sound production mechanisms are concerned, these simplifications being for the most part de­rived from theoretical reasoning based on Lighthill’s acoustic analogy. In what follows we will explore some numerical databases, from which we will endeavour to extract and evaluate the salient source features through the application of a number of different analysis tools. These analyses closely follow the methodology outlined at the beginning of this section; and a de­tailed exposition of the various analysis tools implemented are described in section §5.