COMPLETE SETS OF EOM
Using Equation 3.11 and Equations 3.15 through 3.19, the following nine coupled differential equations describe the aircraft motion in flight.
Force equations:
m(u + qw — rv) — qSCx — mg sin U + T cos sT
m(v + ru — pw) — qSCy + mg sin f cos U (3.20)
m(w + pv — qu) — qSCZ + mg cos f cos U — T sin sT
Moment equations:
qSbCi — p Ix — q Ixy — r/xz + qr(/z — Zy) + (r2 — q2)/yz — pq/xz + rp/xy qScCm — —_/xy + <q/y — r/yz + rp(/x — Iz) + (p2 — r2)/xz — qr/xy + pq/yz (3.21)
qSbC„ — —_ /xz — ^/yz + Г/z + pq(/y — /x) + (q2 — p2)/xy — rp/yz + qr/xz
Euler angles and body angular velocities:
f — p + q tan U sin f + r tan U cos f U — q cos f — r sin f (3.22)
fi — r cos f sec U + q sin f sec U
The above set of equations represents the 6DOF motion of the aircraft in flight. These can rearranged and expressed in two equivalent forms of equations.
3.5.1 Rectangular Form
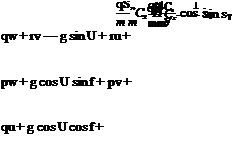 |
|
When the velocity is represented in a rectangular coordinate system, Equations 3.20 through 3.22 can be rearranged to yield the following set of equations in rectangular form:
p = l_ 2 {qSb(IzCi + IxO — qr(I2xz + l2 — Iylz) + pqlxzdx — Iy + Iz)} lxlz 1xz
q = J {qScCm — (p2 — r2)Ixz + pr(Iz — Ix) + T(itx sin St + itz cos St)} (3.23)
Iy
r = l_ 2 {qSb(IxCn + IxzCi) — qrIxz(Ix — Iy + Iz) + pq(12 + iI — Uy)}
IxIz — Ixz
f = p + q tan U sin f + r tan U cos f U = q cos f — r sin f C = r cos f sec U + q sin f sec U
Note that the terms in the rectangular boxes in the expressions for U, v, and w are the linear accelerations. This gives a set of kinematic equations, which can be used to check data consistency and estimate calibration errors in the data. The model equations normally used for kinematic consistency check are
U = —qw + rv — g sin U + ax v = —ru + pw + g cos U sin f + ay w = —pv + qu + g cos U cos f + az
f = p + q tan U sin f + r tan U cos f (3.24)
U = q cos f — r sin f C = r cos f sec U + q sin f sec U h = u sin U — v cos U sin f — w cos U cos f











