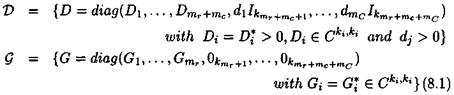COMPUTATION OF SKEWED i BOUNDS

Two mixed v upper bounds and a mixed v lower bound are proposed in this chapter.

1. A FIRST і/ UPPER BOUND

Let Д a mixed structured perturbation (see equation (1.26)). Remem­ber from chapter 5 that the sets V and Q of scaling matrices D and G are associated to Д:

Scaling matrix D must thus satisfy DA = AD.

Let Д = diag(AьДг), where Ді and Д2 are mixed structured per­turbations. Let mi the dimension of Дг. Scaling matrices Dt associated to perturbations Д* are introduced, with ДДг = Д Д■ D 1 and £>2 are then defined as:

so that D = .Di + D2 is a scaling matrix associated to perturbation Д. Proposition 1..1 presents a first mixed v upper bound (see subsection 2.1 of chapter 5 for the definition of the quantities A (A, B) and r)(A, B)).

PROPOSITION 1..1 (Ferreres and Fromion, 1997)

u(M) < л /max(0, inf + Di)M – Dl + j(GM – M*G),D2)) (8.3)

у Di,£>2iC

Remarks:

(i) The optimal values of scaling matrices Z>i, D2,G in Proposition 1..1 can be computed with recent methods for solving LMIs: see chapter 5 (subsection 2.1).

(/’/’) The v upper bound of (Fan and Tits, 1992) is recovered when the model perturbation A only contains full complex blocks.

(in) The classical p upper bound of (Fan et al., 1991) can be obtained in Proposition 1..1 by taking Ai empty, so that Di = 0.

It is possible under mild conditions to compute the exact value of v by computing recursively the exact value of p (see subsection 4.2 of chapter 1). Analogously, Proposition 1..2 claims that it is possible to compute the и upper bound of Proposition 1..1 by computing recursively the /і upper bound of (Fan et al., 1991).

PROPOSITION 1..2 (Ferreres and Fromion, 1997) Let:

IfvuB(M) < oo, then vub(M) is the unique limit of the fixed point iterationafc+i = h(otk), where h is defined as: