DIRECT COMPUTATION OF THE MAXIMAL S. S. V

When applying fj, analysis to the standard interconnection structure M(s) — A(s), the s. s.v. m ( M(jw) ) is classically computed as a function of д using a frequency gridding, and the robustness margin is deduced as:

kmax = min l/fx&(M(jw)) (7.9)

UJ

However, especially in the case of flexible systems, narrow and high peaks may appear on the p, plot, so that only a prohibitively fine frequency gridding could find them (Freudenberg and Morton, 1992). An attract­ive solution in this case is to directly compute the maximal s. s.v. over the frequency range, or – more interestingly – over small frequency in­tervals (Ferreres and Fromion, 1997). As illustrated briefly below, this maximal s. s.v. can be computed as the solution of an augmented skewed p, problem.

The idea is to treat the frequency as an additional uncertainty. A possible solution is provided by the following Lemma: see (Ferreres and Fromion, 1997) and included references, see also (Doyle and Packard, 1987; Helmersson, 1995) for alternative methods.

LEMMA 3..1 Let (A, B,C, D) a minimal state-space model of the asymp­totically stable transfer matrix M(s). There exists a frequency uj Є [w, w and a perturbation Д satisfying det(I — M(jw)A) = 0 if and only if there exists an augmented perturbation A satisfying det(I — HA) = 0 with:

6w = ^ Є [0,1]

u> — W

6wlm 0 ‘

: 0 Д

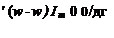: HflHX

jA~l A~lB

—jCA~l —CA~lB + D

0 ■ 0

Let цтах the maximal s. s.v. /j,(M(ju>)) over the frequency interval [tu, й>]. The following Proposition claims that the computation of цтах is a skewed /x problem: see also (Ferreres et al., 1996b) for an alternat­ive skewed Ц problem, in which the frequency is treated as a one-sided uncertainty [9].

Proposition 3..2

Umax = 1 /тіп(к / ЗД = diag(Sw, kA) with Su € [0,1], Д Є BA

and det(I – HA) = 0)

6w is thus maintained inside the interval [0,1], while the initial model uncertainty Д belongs to the expanded or shrunk ball кВА.

In the context of the robustness analysis of a flexible system, a first solution is thus to handle an augmented skewed /x problem in order to dir­ectly compute the maximal s. s.v. over a frequency interval. Nevertheless, we focus in this book on an alternative approach, which is computation­ally more efficient and which gives yet good results in practical examples: see chapter 10 and (Ferreres and Biannic, 1998a).