Effects of Mach Number
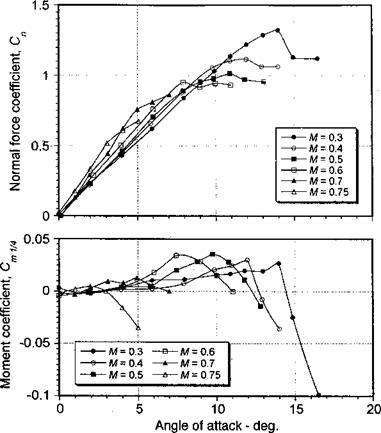
As described previously, airfoil characteristics at Mach numbers above about 0.3 are affected by the compressible nature of a real flow. As an example, the effects of Mach number on the lift and pitching moment characteristics of a NACA 0012 are shown in Fig. 7.38. Two effects are immediately noticeable. First, there is an increase in the lift-curve – slope with increasing Mach number. This is the well-known Glauert effect, as discussed previously in Section 7.6.3. Physically, the effect occurs because pressure disturbances cannot propagate as far upstream in a given time as the Mach number increases. This increases the streamline curvature near the leading edge of the airfoil and manifests as an increase in the effective AoA. Second, the value of maximum lift coinciding with the break in the pitching moment curve tends to decrease with increasing Mach number. This is because of the onset of flow separation produced by the high adverse pressure gradients near the leading edge at low free-stream Mach numbers or near the shock wave at higher Mach numbers.
To explain airfoil behavior at higher Mach numbers, consider the presentations given in
T^rto n ao оn лп n an
1150. cuiu /.-tv. 115Ш& /,J7 anuwa ui ui& uiduiuuuuii uu the NACA 0012 for a range of angles of attack at a free-stream Mach number of 0.64. As the AoA is increased from 0 to 2°, the flow at the leading edge of the airfoil becomes mildly supercritical (locally supersonic). Under these conditions the flow returns to subsonic conditions by passing through a shock wave before reaching the trailing edge. With increasing AoA, the extent of supercritical flow increases and the shock wave moves further aft on the chord and strengthens. However, as the AoA reaches 6° the shock wave becomes more oblique to the airfoil surface and starts to move forward. The pressure behind the shock also decreases as reflected in the “break” in the pitching moment shown in Fig. 7.38. This indicates the onset of flow separation. However, the flow reattaches again some distance
![]()
|
|
|
|
Figure 7.40 Effect of increasing free-stream Mach number on the upper surface pressure distribution of a NACA 0012 airfoil at a constant AoA of 8°. Data source: Bingham & Noonan (1982). |
downstream of the shock wave, in effect producing a turbulent separation bubble. This bubble is conceptually similar to a laminar separation bubble and contains a region of low velocity, constant pressure, recirculating flow. During this process, the lift coefficient shows a departure from the linear С/ versus or behavior but continues to increase with increasing AoA.
Figure 7.40 shows the upper surface pressure distribution over the leading edge region of the NACA 0012 for a series of increasing values of free-stream Mach number when the airfoil is held at a constant AoA of 8°. As is increased from 0.43 to 0.48, the subsonic form of the pressure distribution changes as the flow near the leading edge becomes mildly supercritical and the steepest adverse gradient moves aft to about 20% chord. With further increases in M^, the shock wave strengthens and moves further aft as the extent of supercritical flow increases. Eventually at M^ — 0.64, the shock becomes sufficiently strong to produce flow separation, which causes the shock to move forward on the chord and to become more oblique to the airfoil surface. Again, the flow reattaches forming a turbulent separation bubble. Further increases in causes the bubble to lengthen, and eventually the boundary layer will fail to reattach, producing complete flow separation over the upper surface of the airfoil. This is called shock induced stall.
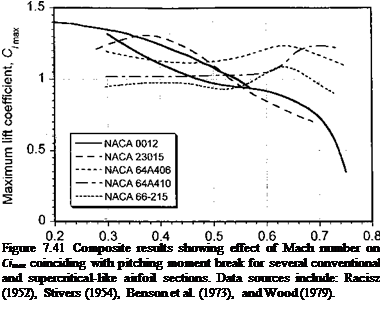
Figure 7.41 shows the effect of Mach number on the maximum value of lift of the airfoil for nominally attached flow. Because the lift continues to increase after the onset of flow separation, these values have been derived by determining the value of С/ corresponding to the break in the pitching moment curve (i. e., the initial onset of flow separation), which will also be coincident with a rapid increase in drag. For lower values of the curves are relatively flat and the airfoils retain their maximum lift, although the effects of compressibility clearly cause the values of Qmax to decrease with increasing Mach number. For values of Moo greater than about 0.5, the onset of supercritical flow causes the maximum values of lift to quickly decrease for further increases in M00, at least for the NACA 0012 and NACA 23015 airfoils. At the lower Mach numbers, the camber of the NACA 23015 airfoil increases the value of C/max relative to the NACA 0012, but this advantage is lost at the higher
Free-stream Mach number, M
 |
1 00
Mach numbers because the camber and slightly greater thickness gives the NACA 23015 airfoil a lower critical Mach number. For the higher Mach numbers, the range of angles of attack over which the airfoils can operate without some flow separation is considerably
rcuUCcu.
While most airfoils show a steady reduction of maximum lift coefficient with increasing Mach number, not all airfoils behave this way. Figure 7.41 also shows the Qmax behavior of the NACA 64-series and 66-series airfoils. While the values of C/max attainable by this airfoil at low Mach numbers is inferior to either of the NACA 0012 or 23015 airfoils, there is a beneficial effect on C/max at the higher Mach numbers. The NACA 66-215 and 64- series airfoils have a point of maximum camber fairly far aft, and so these airfoils exhibit a higher critical Mach number and a favorable effect on the strength of the developing shock wave. This is similar to the behavior of supercritical airfoils, the ideas of which have been introduced previously. Improved airfoils for transonic flow applications were originally devised by NASA – see Whitcomb & Clark (1965) and Whitcomb (1976). To achieve this behavior, the leading edge geometry (thickness and camber) must be shaped to produce a longer run of supersonic flow but a weaker recovery shock. These conditions, however, can generally only be obtained for very specific combinations of angles of attack and Mach numbers. For other “off-design” operating conditions these airfoils usually suffer lift and
__ л _______ „—____ *_______ _
uiag pwiaiuca. oupgiuiuLai auiuua nave; ueeu udeu iui luauty уьаїй uujei uau^puu auuau,
and “supercritical-like” sections are used as tip sections on some helicopters. At subsonic speeds, supercritical airfoils can exhibit higher leading edge suction peaks and are likely to encourage stall at lower angles of attack compared to conventional airfoils and thus would not be suitable for the inboard parts of helicopter blades.
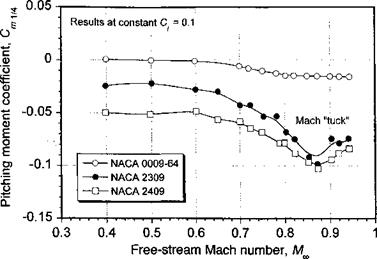
As previously discussed, the effects of compressibility initially cause the aerodynamic center to migrate slightly forward with increasing Mach number. As the flow becomes supercritical and then transonic, the aerodynamic center shifts more quickly rearward resulting in the Mach tuck phenomenon – see Abbott & von Doenhoff (1945), Dadone & Fukushima (1975), and Prouty (1986). Mach tuck manifests as a rapid increase in nose-down pitching
|
Figure 7.42 Effect increasing free-stream Mach number on the pitching moment at constant lift coefficient for several NACA series airfoils. Data source: Ferri (1945) |
moment for a relatively small change in Mach number. If Mach tuck occurs on the advancing tip of a rotor, then it may produce high blade and control loads and may effectively limit the helicopter’s forward flight speed. For most airfoils, the onset of Mach tuck appears at a slightly higher Mach number after drag divergence as the shock waves begin to strengthen and move more rapidly aft on the airfoil surface.
Because it is possible for the rotor to exceed the tip drag divergence Mach number under various flight regimes such as during dives and certain maneuvers, it is obviously desirable to minimize the nose-down pitching moment trend to as high a Mach number as possible. The data in Fig. 7.42, taken from Ferri (1945), compare pitching moment results at a constant Q =0.1. Figure 7.42 shows that the nose-down trend in the pitching moment is minimized for symmetric airfoils. Experiments have shown that camber applied further to the rear of the airfoil generally results in more severe “tuck” problems than for an airfoil with nose camber. The increased pitching moment is caused by changes in the relative chordwise pressure distributions on the upper and lower surfaces of the airfoil that result from the development of supercritical flow and shock waves. Thus supercritical airfoil design techniques are often used to minimize the strength of the shock wave and can delay the Mach tuck problem on the airfoil to higher free-stream Mach numbers.
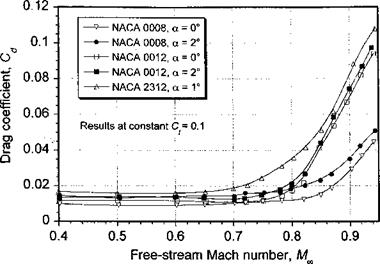
Figure 7.1 has shown that the tip of the advancing blade operates at low lift but at high Mach numbers. Therefore, from a rotor power consumption point of view the drag characteristics of the airfoil when it operates at high Mach numbers are also important. Figure 7.43 shows the drag characteristics of several airfoils as a function of Moo• In the low Mach number range, the drag stays nominally constant or may decrease slightly because of an interdependent effect of increasing Reynolds number. It is only when the critical Mach number is reached that the drag shows a more rapid rise. This drag rise occurs at progressively lower Mach numbers as the thickness-to-chord ratio of the airfoil is increased. A similar effect is obtained by increasing the AoA. The effect of camber also decreases the critical Mach number and so reduces the Mach number at which the drag rise occurs compared to symmetric airfoils of the same thickness-to-chord ratio.
|
Figure 7.43 Effect of increasing ffee-stream Mach number on the drag of several NACA series airfoils. Data source: Ferri (1945) |
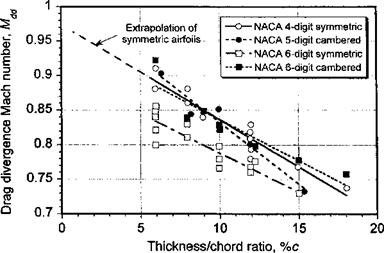
The value of Mqo at which the drag coefficient begins to rapidly increase is known as the drag divergence Mach number, Mdd – Physically, drag divergence occurs because of an entropy loss through the shock wave coupled with additional pressure drag as a result of boundary layer thickening and shock induced separation. Nitzberg & Crandall (1949) discuss the phenomenon in detail. The value of Mdd is often defined in as the Mach number for which dCd/dMpo > 0.1 or, alternatively, the Mach number for which the drag coefficient becomes twice its incompressible value [see Prouty (1986)] at the same Q or a. The drag divergence Mach numbers of airfoils at zero lift are plotted in Fig. 7.44 as a function of
|
Figure 7.44 Drag divergence Mach numbers of several NACA series airfoils at zero lift. Data source: Collated information by Prouty (1986). |
thickness-to-chord ratio. It can be readily observed that thinner airfoils have a much higher drag divergence Mach number and so will be the best choice for the blade tip region.