GAIN-SCHEDULED AND ADAPTIVE ROBUST CONTROL

Local properties of a gain-scheduled control system can be analyzed with the p and и tools. Let в the vector of scheduling parameters: the

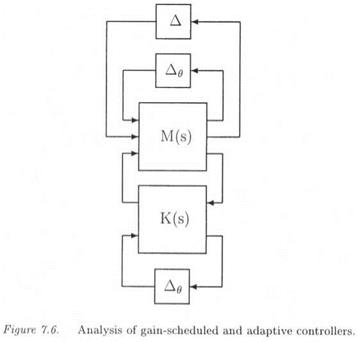
plant and controller can generally be expressed as LFTs involving a diag­onal matrix Ae, which contains possibly repeated parameters 0i(Ferreres et al., 1995). The augmented plant of Figure 7.6 is the closed loop ob­tained by connecting both LFTs. A structured perturbation Д is added to account for model uncertainties and performance blocks. Since the range of variation of the scheduling parameters is generally known a priori, a skewed /і problem is obtained, i. e. Ag is maintained inside its prescribed range of variation, while the size of Д is free.

An other skewed /л problem is obtained by introducing uncertainties 66i in the scheduling parameters 6f. the maximal allowable value of 86 is then computed, such that local stability or performance of the control system is guaranteed for all в belonging to a prespecified set. Note fi­nally that adaptive robust controllers can be analyzed in the same way (Ferreres et al., 1995).