Global Characteristic Properties of Attached Viscous Flow

In order to identify the global characteristic properties of attached viscous flow, we need to have a look at the characteristic properties of the boundary- layer equations [1]. We do this for convenience by assuming incompressible and first-order boundary-layer flow. Following [13], we introduce characteris­tic manifolds p(x, y, z), for instance like

d _ dp d, _ d,

dx dxdp ^dp ( ‘ ^

into eqs. (7.36) to (7.39).

After introduction of the kinematic viscosity v = р/р and some manipu­lation the characteristic form is found

with the abbreviation

Д = ufix + vfiy + wfiz. (7.43)

The pressure gradients dp/dx and dp/dz do not enter the characteristic form, because the pressure field is imposed on the boundary layer, i. e., dp/dx and dp/dz are forcing functions.

Eq. (7.43) corresponds to the projection of the gradient of the manifold onto the streamline, and represents the boundary-layer streamlines as char­acteristic manifolds. To prove this, we write the total differential of <p

dfi = fixdx + fiy dy + fiz dz = 0, (7.44)

and combine it with the definition of streamlines in three dimensions

in order to find

dp = upx + vpy + wpz = A =0. (7.46)

Thus it is shown that streamlines are characteristics, too.

The remaining five-fold characteristics py in у-direction in eq. (7.42) are typical for boundary-layer equations. These characteristics are complemented by two-fold characteristics in у-direction coming from the energy equation, eq. (7.40), which we do not demonstrate here. These results are valid for compressible flow, too, and also for second-order boundary-layer equations.

Boundary-layer equations of first or second order, in two or three di­mensions, are parabolic, and hence pose a mixed initial condition/boundary condition problem.[90] Where the boundary-layer flow enters the domain under consideration, initial conditions must be prescribed. At the surface of the body, у = 0, and at the outer edge of the boundary layer, у = 5, boundary conditions are to be described for u, w, and T, hence the six-fold character­istics in у-direction. For the normal velocity component v only a boundary condition at the body surface, у = 0, must be described, which reflects the seventh characteristic.

We have introduced the boundary layer as phenomenological model of attached viscous flow. This model is valid everywhere on the surface of a flight vehicle, where strong interaction phenomena are not present like separation, shock/boundary-layer interaction, hypersonic viscous interaction, etc.

In Sub-Section 7.1.1 we have noted the three viscous-flow phenomena, which are directly of interest in vehicle design. If attached hypersonic viscous flow is boundary-layer like, we can now, based on the above analysis, give a summary of its global characteristic properties, see also [1]:

— Attached viscous flow is governed primarily by the external inviscid flow field via its pressure field, and by the surface conditions.

— It has parabolic character, i. e., the boundary conditions in general dom­inate its properties (seven-fold characteristics in direction normal to the surface), the influence of the initial conditions usually is weak.

— Events in attached viscous flow are felt only downstream, as long as they do not invalidate the boundary-layer assumption. This means, for instance, that a surface disturbance or surface suction or blowing can have a magni­tude at most of 0(1/у/Reref). Otherwise the attached viscous flow loses its boundary-layer properties (strong interaction).

— In attached viscous flow an event is felt upstream only if it influences the pressure field via, e. g., a disturbance of O(1) or if strong temperature gradi­ents in main-flow direction are present (d(kdT/dx)/dx and d(kdT/dz)/dz = O(Reref). The displacement properties of an attached boundary layer

are of 0(1/^/Reref), and hence influence the pressure field only weakly (weak interaction) [1].

— Separation causes locally strong interaction and may change the onset boundary-layer flow, however only via a global change of the pressure field. Strong interaction phenomena usually have only small upstream influence, i. e., their influence is felt predominantly downstream (locality principle [1]) and via the global change of the pressure field.

— In two-dimensional attached viscous flow the domain of influence of an event is defined by the convective transport along the—straight—stream – lines in downstream direction. Due to lateral molecular or turbulent trans­port it assumes a wedge-like pattern with small spreading angle.

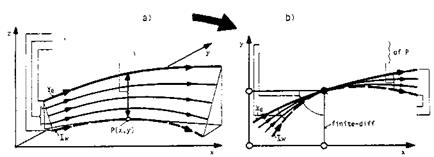
— In three-dimensional flow, the influence of an event is spread over a domain, which is defined by the strength of the skewing of the stream surface, Fig. 7.3. The skin-friction line alone is not representative. Of course also here lateral molecular or turbulent transport happens. If a boundary-layer method is used for the determination of the flow field, it must take into account the domain of dependence of a point P(x, y) on the body surface, which must be enclosed by the numerical domain of dependence, Fig. 7.3 b).

view from above

*p(x»y)

skin-friction 1ine — external stream! ine – . molecule о data known • data to be computed

Fig. 7.3. Three-dimensional boundary layer with the skewed stream surface (schematical) [3]. Note that in this figure x, y are tangential to the surface, and г is normal to it): a) the streamlines as characteristics, b) domains of dependence and of influence of flow properties in P(x, y).