Insertion of Additional Support Points

The solution accuracy and the robustness of the MLS projection algorithm im­proves with increasing number of support points, but only if these offer sufficient information density in all spatial directions. Moreover, with higher number of sup­port points necessarily also the support radius becomes larger; hence the desirable locality of the projection diminishes. These two problems can be alleviated by us­ing an idea also put forward by Quaranta et al. [23]: It is not the actual nodes of the

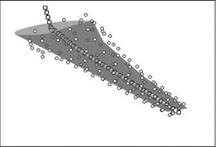
Fig. 5 left: Arrangement of the “fishbones” generated for a beam model. The structural nodes are represented by squares, the edge midpoints by diamonds and the additional support points by circles. Here the radius rFB is fixed to a value approximately half the average chord length. The number of additional support points per edge midpoint nFB is set to five, which is the recommended value for beam models. right: Arrangement of the additional support points after alignment with the wetted surface.

structural model that are taken as supports for the interpolation. Instead, the midpoints of the beam elements, or respectively the edge midpoints of higher­dimensional elements are used. Surrounding these points, additional supports are in­serted circumferentially, as shown in the left image of Fig. 5. Quaranta et al. coined the term “fishbones” for this arrangement. The additional support points not only as­sure adequate information distribution in all spatial directions, but also allow for the simple projection of rotational deformational components at the structural nodes: The rotations are interpolated to the edge midpoints and result in a translation of the additional support points according to their radius rFB. During the converse pro­jection of loads from the wetted surface to the structure the forces projected to the additional support points are combined at the edge midpoints and corresponding off­set moments are introduced. The loads at the edge midpoints are then split between the adjacent structural nodes.

The GSB and MLS projection methods were further enhanced by enabling an automatic alignment of the additional support points with the wetted surface, as shown on the right of Fig. 5. To this end, the information which surface points are in the vicinity of each edge midpoint is required. Therefore, in a preparatory step the mapping of supporting edge midpoints to surface points is inverted. The shape of the surface section normal to a given edge is approximated as an ellipse. The additional support points are then inserted along its circumference with equiangu­lar spacing. Special attention is needed when the wetted surface does not cover the whole circumference, like along the fuselage of a half-model suspended in the sym­metry plane.