Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
Integral Boundary Layer Solution
4.11.1 Thwaites method Assumptions and formulation
 |
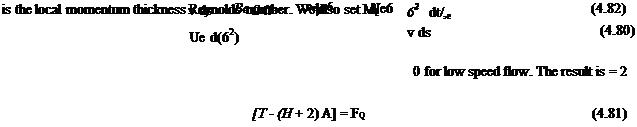The Thwaites method [21], [11], [12] solves the classical low-speed laminar boundary layer problem by assuming specific functional forms for Cf, H, and the entire righthand side of the von Karman equation (4.28). This is first manipulated by multiplying 2Req x [equation (4.28)], where
 |
 |
 |
 |
 |
 |
 |
where T is a normalized wall shear, and A is a normalized edge velocity gradient or equivalently a normalized pressure gradient. For the power-law flow case ue = Csa these are also products of Falkner-Skan solution parameters, and also of the normalized velocity profile derivatives at the wall.
Their numerical values are listed in Table 4.1. Also listed is the entire righthand side parameter combination Fq in the manipulated von Karman equation (4.81).
For power-law flows, all the Falkner-Skan parameters (columns of Table 4.1) are functions of the exponent a, or more generally functions of each other. The key assumption of Thwaites’s method is that the A), Ffl(A) relations arc valid for any boundary layer flow, not just a power-law flow. In effect this assumes that the boundary layer profile U{iy, s) at each s location has the same shape as one of the Falkner- Skan profiles. That is, if A is known at a location s in a general flow, then H, T, Fq at that location are also immediately known from the corresponding row in Table 4.1.
Explicit integration
Rather than use the Falkner-Skan solutions in Table 4.1, Thwaites examined a number of other theoretical flows to quantify these functions. For Fe he chose
Fe(A) = 0.45 – 6A (4.84)
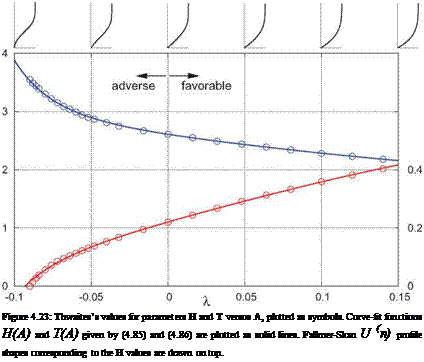
which doesn’t quite match the values in Table 4.1, but it is close. His H and T were provided in tabulated form. They are shown in Figure 4.23, and are closely approximated by the following convenient curve fits.
Я, л, = 2.61-4ЛА + 14А* + р24^_
 |
T, a, = Um + l-m-SA’-jOTP
Strictly speaking, equation (4.81) could be numerically integrated using only the T(A) and H(A) functions inserted in its righthand side. However, the fact that their combination Fe(A) is very nearly linear allows a simpler explicit solution. When the approximate Fe(A) given by (4.84) is inserted for the entire righthand side of equation (4.81), and the entire equation is then multiplied by vu5, its lefthand side becomes a perfect differential which can then be explicitly integrated.
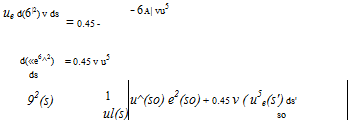(4.87)
 |
 |
 |
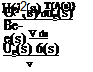If ue(s) and v are provided, the corresponding 9(s) can be immediately obtained by evaluation of the integral in (4.87), numerically if necessary. This 9(s) is then used in the closure relations to obtain the remaining quantities of interest.
In general, the integral in (4.87) is evaluated from some initial location s0 where 9(s0) must be specified. But if this s0 is the sharp leading edge of a Blasius flow, then 9(so) = 0. Alternatively, if s0 is at a blunt leading edge stagnation point, then ue(s0) = 0, in which case 9(s0) in (4.87) is immaterial. Hence, in both of these typical situations no initial data is required.
