LEADING-EDGE SOLUTION

The second-order solution of Eq. (7.37) shows that the perturbation expansion for the thin airfoil breaks down in the neighborhood of the round leading edge in a region whose extent is measured by the leading-edge or nose radius of the airfoil r (r is the radius of curvature at the leading edge). Also, r is 0(e2). To illustrate the correct local solution in the neighborhood of the leading edge, let us consider a symmetric airfoil at zero angle of attack. Introduce the coordinate s = x + c/2, which is measured from the leading edge (Fig. 7.3). Many symmetric low-speed airfoil sections are analytic in the leading-edge region and their surfaces can be described by

z = ±T0sm ± 7[s3/2 ± • • • (7.38)

where T0, 71, . . . are constants.

For small values of s [or for s = 0(e2)], the surface is given by the first

term

z = ±VT%s (7.39)

which is seen to be identical to the equation of a semi-infinite parabola, which can also be given by

z = ±V2ra (7.40)

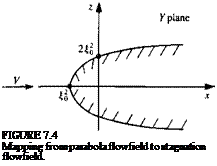
The local solution then is the symmetric flow past this parabola whose

geometry is shown in Fig. 7.3 and since this solution is not valid in the far field, let us for the moment denote the stream speed as V. The method of conformal mapping will be used to obtain the surface speed on the parabola. Consider the mapping

Y=-f2=ti2-?-2i£r, (7.41)

where Y = x + iz and / = £ + ir). Then it can be seen that the curve f = £0 in

the / plane maps into the parabola

z = ±V5fW+Ш) (7.42)

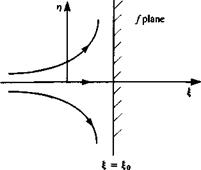in the Y plane and the corresponding flowfields in the two planes are shown in Fig. 7.4.

The flow in the/plane is seen to be stagnation point flow against the wall § = and its complex potential is

F = — V(f — §0)2 (7-43)

The constant V has been chosen to provide the correct far field solution in the parabola or physical plane. On the surface we have / = іт/, § = §0, and the complex velocity becomes

Now, rj = V* + £o and if we introduce s = x + §o> the surface speed on the parabola is

(7.45)

Note that the surface speed at any point is just the projection of the free-stream speed onto the tangent.

Since the nose radius of the parabola is r = 2§o (Eq. (7.42) yields z = ±V4fo$), the desired local surface speed for the airfoil becomes

The corresponding local solution for the airfoil problem with camber and angle of attack is given in Van Dyke.7 2 We therefore have available two incomplete solutions to the problem we set out to solve at the beginning of the chapter. The thin-airfoil solution has been obtained correct to second order but it is not correct in the neighborhood of the leading edge. The local solution is exact in
the neighborhood of the leading edge but does not describe the flow in the far field and it also contains an undetermined constant.