LONGITUDINAL STABILITY. CHARACTERISTICS OF AIRPLANES

Stability is the built-in tendency of a vehicle to return by itself to a certain state of equilibrium. For example, a railroad vehicle is extremely stable in regard to pitching (and rolling) motions. Ships have considerable stability (based on buoyancy). By comparison, the stability of all types of aircraft is much more sensitive and complex, resting upon the interaction by means of the flow of air between half a dozen component parts, such as wing, fuselage, propulsion system and tail surfaces in particular.

In this and Chapters XII, XIII and XIV the general charac­teristics of aircraft stability will be discussed. In particu­lar, the stability will be covered in terms of the funda­mental parameters for the longitudinal, directional and lateral modes (1). Included in the treatment will be the basis for determining the stability derivatives of the wing, fuselage, tail and propulsion systems. We will also consider static and dynamic stability of simple and plain aircraft configurations.

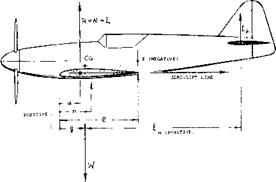
FOR MANY PRACTICAL PURPOSES THE NORMAL FORCES AS SHOWN, APPROXIMATELY EQUAL TO LIFT, CAN BE USED IN STATIC STABILITY. a – TO AERODYNAMIC CENTER OF WING (o) n – TO NEUTRAL POINT OF CONFIGURATION g – TO CENTER OF GRAVITY І-.) Figure 1. Geometry of airplane configuration showing the static balance of weight and aerodynamic forces.

(1) It seems that airplanes were flown for years, before their stability was first formulated by Bryan, “Stability in Avia­tion”, London 1911.

1. FUNDAMENTALS OF LONGITUDINAL STABILITY

Longitudinal motions of an airplane, the motions in a vertical plane, can tentatively be analyzed without refer­ence to motions in other directions, on the simple assump­tion that the craft is kept on course and that rolling is prevented by proper control.

Parameters Involved. The aerodynamic forces and mo­ments of an airplane are function of shape, arrangement and interference of the component parts. Their magnitude and possibly their character, may change as a function of speed (Mach number) and altitude (Reynolds number). The resultant stability may also be affected by structural elasticity of the components and/or the configuration. The operational necessity of control by means of the elevator (hinge moments, weight and strain in the system) will also have an effect upon stability. Longitudinal char­acteristics may be altogether different during the landing maneuver (flaps, landing gear, ground effect). Propulsion by jet engines, propellers, or ducted fans cause dynamic interaction problems which have a very considerable in­fluence upon stability. The stability of aircraft motions also involves mass – aerodynamic forces and aeroelasticy arising as a consequence of such motions. Many or some of the parameters mentioned, may or will, therefore, be affected during the motions of which they are the cause and/or integral part. As a consequence, when including all variations of shape, interaction and operation, the number of parameters possibly to be considered, may reach the order of 100. Stability analysis may thus appear to be an unsurmountably difficult problem, particularly in view of the fact that a longitudinal shift of the center of gravity by plus or minus a very few percent of the wing chord, can be the difference between a stable or unstable air­plane. Fortunately, most of those parameters are of sec­ondary importance; many of them have not even been analyzed and/or tested. Some of them are, on the other hand, are of predominant importance such as downwash and possibly thrust in particular. Indeed, consideration of “a dozen” selected parameters will and has to be suffic­ient in the practical analysis of stability.

Notation. As described in the Chapter I, there is a basic convention regarding positive and negative directions of dimensions, forces and moments. The following symbols and conventions will apply. For an airplane as in figure 1, in the longitudinal plane of symmetry, about and in reference to its center of gravity CO there are the geometric factors:

x = longitudinal distance parallel to the zero-lift line of the mean wing section.

z = distance between the wing’s aerodynamic center and the CG, in normal (vertical) direction.

c = mean aerodynamic chord “mac”, replacing the wing aerodynamically.

distance of horizontal tail quarter-chord point from CG.

H = subscript indicating the horizontal tail.

M = CmqSc = pitching moment, usually about the CG.

CP= center of pressure or lift forces.

AC= aerodynamic center of wing (Cm = constant)

There is also a “neutral” point, representing the aerodynamic center of the wing plus tail configuration.

dynamic forces and moments (due to inertia and/or acceleration) may tentatively be disregarded. By neglecting these contributions, the stability of an airplane becomes the favorable interaction between gravity (weight) and aerodynamic (lifting) forces and moments. This type of stability can easily be determined in a wind tunnel by hinging an airplane model about the lateral axis through the point representing the center of gravity. The slope or strength of the restoring moment dM/doi is then called 4‘static stability”. Such investigations provide indispensable information regarding aerodynamic forces and moments contributed by wing, fuselage, propulsion system tail surface etc. and give an insight into the downwash and wake effects. The investigations lead to practical measures of changes necessary for improving stability. Disregarding extreme conditions (such as particularly in more or less “ballistic” missiles) static stability is the most important component of dynamic stability; and as far as airplanes are concerned, static stability can be said to be a prerequisite of dynamic stability.

The Signs The following sign convention will be used in this text: lift and drag = positive “up” direction = positive nose-up moment = positive wind direction = positive downwash velocity = negative

In particular, a positive pitching moment tends to increase the angle of attack, thus leading to stalling. A positive value of the derivative dCyJdoc or dC^dCu. , means a lack of stability. Therefore, to be stable, every airplane should have a negative pitching moment derivative. The definition of moment arms is more difficult. As far as geometry is concerned, we will consider the distance of any point on the chord of a wings (or on the axis of a fuselage body) aft of the leading edge (or the nose, respectively) to be positive. However, when it comes to pitching moments due to positive lift forces, usually about the CG, the moment arm of the horizontal tail must evidently be counted as negative, while that of the wing (assuming that the CP is ahead of the CG) has a positive value.

Static Stability. The oscillatory motions of an airplane in longitudinal direction (pitching, heaving, variation of speed) can properly be described by a set of equations. Assuming, however, that the motions may be sufficiently slow (thus eliminating all derivatives against time), the

Balance. In airplanes, usually one of the less important parameters contributing to stability is drag. To simplify the consideration of balance and stability, we will thus assume the basic system of forces and moments as in figure 1. Specifically, the lifting or resultant forces are assumed to be normal to the wing section’s zero lift line, through its aerodynamic center AC (which means approxi­mately through the trailing edge). All dimensions are measured in directions parallel or normal to that line. For Cm =0, longitudinal characteristics of the “airframe” are then described by a pair of simple equations, the first of them indicating balance:

L(Ax) + LH zero; L(ax) = L/Th (1)

where the first term represents the pitching moment of the wing and the second term that of the horizontal tail. For forces and positions as illustrated in figure 1, the moment arm ax = g — a, has a positive value, while that of the tail must be counted to be negative. In the form of non-dimensional coefficients (based on wing dimen­sions) balance is defined by

CL (іх/с) = сш (SJS)UJc) (2)

where (SH /S)( J! jc) = vw = horizontal-tail “volume” (be­cause it has the dimension of ft3).

Basic Stability Equation. A second equation describes the variations of forces and moments, as the airframe is slowly rotated (at constant tunnel speed V) about the transverse axis through the CG. For a vertical distance (see figure 1) z = 0, the airplane is then stable, provided that

(dLw /doc)Ли/с I ;> (dl/doc )(Дх/с) (3)

where Ax/c as above, = g — a. Replacing the lift by its coefficient “CL{y and by CLH q(SM/S), stability is indicated by

(dCLW/doc)Vw > (dCL /doc)(Ax/c) (4)

where VM as above. On the basis of these equations, any type of combination of two “wings” might be made “stable”, including tandem and canard configurations. The reasons for preferring one particular type, larger wing plus comparatively small horizontal tail aft for airplanes are:

1) concentration of lift in one large-span wing is most efficient,

2) a “small” horizontal surface is sufficient for stabili­zation,

3) location at the tail promises longitudinal control up to and beyond CLx,

4) location within the propeller slipstream provides improved control at low speeds, such as on the ground.

Equation (4) also means that for longitudinal stability, the sum of the two sides, equal to the derivative of the complete system (for example, with fixed elevator) must be negative; thus:

(dCm/dCL ) = (dCJdocXdoc /dCL ) ^ 0 (5)

Free Moment. Provided that the wing section is cambered (or owing to the deflection of wing flaps) there is usually a free moment indicated by Cm0 = MQ/qSc (independent of lift, and thus also at zero lift). Including this com­ponent, equation (2) reads in non-dimensional form:

Cmg = Cmo+ ((g — a)/c) CL + Cmw = 0 (6)

where g = longitudinal location of the CG, while a = location of the aerodynamic center (including the influ­ence of the fuselage, etc.). The free moment is thus balanced by the horizontal tail. In a conventional airplane configuration, Сгпн is adjusted by suitable deflection of the elevator so that balance is obtained for a particular lift coefficient, corresponding to speed or dynamic pressure when flying. It should be noted, however, that as a con­stant if not changed by slipstream effects, Cm<>does not affect stability. This is the distinction between balance and stability.

Although the equations presented above for the static stability case are simple, determination of the longitudinal stability of an airplane in complex because

(a) various interference effects that cannot be dis­regarded,

(b) the wing downwash has a large effect on the re­sultant lift curve slope of the horizontal tail sur­face,

(c) forces of, and interference by the propeller (or the propelling jet) are needed in the operation of pow­ered airplanes.

Only the simplest type of configuration without wing flaps and without propulsion effects will be considered in the following sections of this chapter. The influence of the propulsion system on longitudinal stability is covered in Chapter XII.

DYNAMIC LONGITUDINAL STABILITY. After an air­craft is disturbed from its flight path two basic motions are obtained: 1) a long-period or phugoid oscillation and 2) a short-period oscillation. These oscillations may be developed even though the static longitudinal stability of the aircraft is satisfactory. The long-period phugoid oscil­lation may involve several seconds depending on the par­ticular airplane. This motion is normally hardly noticed by the experienced pilot who automatically damps it out with the stick or power changes. The short-period oscil­lation, however, must be adequately damped in the basic airplane system for satisfactory dynamic longitudinal sta­bility. If the airplane has an undamped short period oscil­lation, attempts to correct the difficulty can lead to pilot induced oscillations, PIOS, which accent the unstable con­dition.

The analysis of the dynamic stability problem requires the use of the basic equations of motion and the identi­fication of many stability derivatives. With the stability derivatives involving velocity, angle of attack, q, elevator angle, compressibility, moments, etc. the dynamics of the airplane are analyzed for at least the stick fixed and stick free cases. The development of the basic equations of motion and their analysis in terms of dynamic stability are covered in many available sources, for instance (2,fog) and, therefore, will not be repeated here. Rather a basic understanding of the static longitudinal problem is con­sidered. From the material presented, the derivatives need­ed for the dynamic analysis can be determined with a greater degree of accuracy.