Low Aspect Ratio Wing

Let us study the unsteady aerodynamic forces for the time dependent motions of low aspect ratio wings.

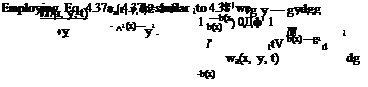For the thin and low aspect ratio wing as shown in Fig. 4.6 with its top and side views, we can make our simplifying assumptions as we did for the steady case to obtain the time dependent downwash expression in terms of the perturbation potential difference as follows

The lifting pressure coefficient for the unsteady flow was

2 0 * 2 0 /.it

cp = —г —Дф H———– тгДф

Pa U2 0t Y U 0x Y

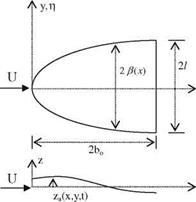Fig. 4.6 Low aspect ratio wing

y,

Here, Аф'(х, у, t)=

—b(x)

For the simple harmonic motion the downwash expression in terms of the surface equation

Wa(x, y) = iO)Za(x, y) + U^Za(x, y)-

The amplitude of the lifting pressure in terms of the perturbation potential reads as

2 2 0

cPa = U^ixA/0 + U ОХАф0 (4-64b)

If we allow elastic deformation and the camber only in chordwise direction, the downwash in Eq. 4.63 becomes independent of y; therefore, the integral becomes py. Accordingly, from 4.63 for the amplitude of the perturbation potential we obtain

Lifting pressure coefficient from 4.64a, 4.64b reads as

(4-66)

In Eq. 4.66 if we take frequency as zero, we obtain Eq. 4.40 which was given for the steady case. The second term of the right hand side of 4.66 gives the phase difference between the lifting pressure coefficient and the wing motion.

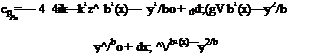Now, we can express 4.66 in more convenient form using the reduced fre­quency, k = xbo/U, and the nondimensional coordinates with superscript * written in term of root half chord, bo, as follows

The second term of the right hand side of Eq. 4.67 is the apparent mass term. In order to satisfy the Kutta condition this term needs to go to zero at the trailing edge. To remedy this and to be in accord with the experimental findings the lifting pressure coefficient is multiplied with an empirical factor (BAH 1996) given as

/ 21/2

F(x) = 1 – x* . (4.68)

Example 4: The wing given in Example 2 is undergoing a simple harmonic motion with h = heixt. Find the lifting pressure on the wing surface in terms of the wing geometry and the reduced frequency.

Solution: Using the fixed vertical amplitude and the wing geometry b(x) = (l/bO)x/2 in 4.67 we obtain

cPa = 4k2h* li1(x)-y2/bo — ikh*j->Vb (x)- y2/bo)

CPa = 4k2 hJ l*2 x*2 /4 — y2/b2 — ikh*—y/1*2 x*2 /4 — y2/b2.

The empirical relation 4.68 is used as a multiplier to satisfy the Kutta condition