METHOD OF IMAGES

Since the solution for the flow past bodies of aerodynamic interest can be represented by suitable distributions of singular solutions to Laplace’s equa­tion, it is important to study the representation of these singular solutions in the presence of additional boundaries, mainly straight, to be able to deal with ground planes and wind-tunnel walls, etc.

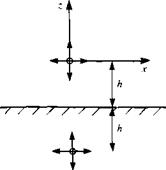
As an example, consider a two-dimensional source of strength a a distance h from a plane wall as shown in Fig. 6.20. Introduce a cartesian coordinate system whose origin is at the source and whose x axis is parallel to the wall. In the absence of the wall, the velocity potential of the source is

Ф = ■£- In Vx2 + z2 (6.76)

2 л

Since we would expect that the only singularity in the flow field is due to

the source, we look for a solution of the form

Ф = — Іп^^+^ + Ф, (6-77)

2 л

where Ф, satisfies Laplace’s equation, has no singularities for z > – A, decays at infinity, and exactly cancels the normal component of velocity at the wall due to the source so that the wall boundary condition is satisfied. The boundary condition on Ф/ is therefore

From symmetry considerations, an “image” source at (0, -2A) is investigated as a possible solution. Its velocity potential is

Ф/ = In V*2 + (2 + 2A)2 (6.79)

2k

and substitution into the boundary condition at the wall shows that it is satisfied. Similar image solutions for a doublet and a vortex are shown in Fig. 6.21. The complex potentials for the original singularities plus their images are

ІГ ІГ

— In F – — ln(F + 2ift) 2л 2л

Next consider a source placed midway between two parallel walls a distance h apart. An image source at (0, h) will satisfy the boundary condition on the upper wall but now both the original source and this image source must be canceled at the lower wall to satisfy the boundary condition there. Images at (0, – ft) and (0, -2A) will take care of the lower wall but now two more images are needed for the upper wall and the process will continue until the complete image system plus the original source consists of an infinite stack of sources a distance ft apart as shown in Fig. 6.22. The complex potential for this source stack is

F(Y) = [In Y + In (F – ift) + In (F + ift) + In (F – 2ift) + In (F + 2ih) + • • •] 2 л

(6.83)

Each pair of images can be combined as

FIGURE 6.22

Image of source midway between parallel walls.

and if the constant terms are neglected, the complex potential becomes

^

The use of the following identity from Gradshteyn and Ryzhik (Ref. 6.5, p. 37),

sinh A = А П (l + рУ (6.85)

leads to the closed-form solution for the complex potential as

F( У) = ^ In sinh ~~ (6.86)

2 71 H

For a clockwise vortex of circulation Г between parallel walls, an application of the iterative image procedure previously used for the source leads to the solution shown in Fig. 6.23, which consists of a stack of clockwise vortices at Y = 0, ±2h, ±4h, . . . and a stack of counterclockwise vortices at ±h, ±3h, ±5h,…. From before, the complex potential for the clockwise stack is

(6.87)

The use of another identity from Gradshteyn and Ryzhik,

(6.88)

FIGURE 6.23

Image of clockwise vortex midway be­tween parallel walls.

results in the following complex potential for the vortex between walls:

F( Y) = [In sinh ~ – In cosh ^7-] = In tanh ~ (6.89)

y 2л і 2h 2h 2л 2h

We have considered images of the singular solutions in a plane wall (for ground-effect applications) and between parallel walls (for wind-tunnel ap­plications). Another possible application is the interaction of an airfoil with its wake or the wake of another airfoil (for unsteady motion) and since we have shown that an airfoil geometry can be transformed through conformal mapping into a circle, the image system for a singular solution in the presence of a circle will be studied.

The circle theorem due to Milne-Thomson6 6 states that if the complex potential F,( Y) represents a flow without singularities for Y<a, then

F(Y) = F,(Y) + fl(^) (6.90)

represents the same flow at infinity with a circular cylinder of radius a at the origin. The function Ft(Y) is defined in the following way. “If F^x) is a function that takes complex values for real values of x, Fx(x) is the function that takes the corresponding conjugate complex values for the same real values of x, and FX(Y) is obtained by writing Y instead of x."

Consider the simple example where Ft(Y) = UY, a uniform stream in the x direction. FX(Y) is seen to be also UY and therefore the flow of the uniform stream with a circle at the origin is given as

a2

F(Y) = UY+U~ (6.91)

which is simply the stream plus doublet solution previously derived. Now let

F1(Y) = ^|n(Y-Yo) (6.92)

which is the complex potential for a source of strength a at Y = Y0. FX(Y) is

Fx(Y) = ~n(Y~Y0) (6.93)

and the complex potential for a source outside a circular cylinder becomes (Eq. (6.90))

F(Y) = ~ [in (Y — Y,) +ln (^p — 1^)] (6.94)

The following manipulation will put the above result in the form of a recognizable image system:

F(y)=Shy-y»)+in(7-f»)]

‘s[ln<y^w + ,"l+,n(y-0-1)]

= ^ [In (Y – Y0)] – In Y + In (y – j-j (6.95)

where the constant terms have been neglected. It can be seen that the solution consists of the original source, an image source of the same strength at the image point, and a sink of the same strength at the origin. These three singularities line up along the same radial line from the origin, as can be seen by writing the location of the image point as

fl2_fl2Yo / a2

Y0 Y0Y0 |Y0|2/ 0

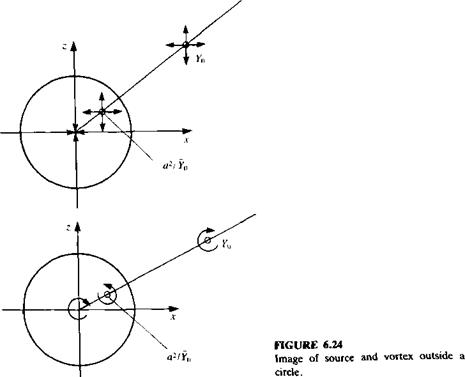
For a clockwise vortex of circulation Г at Y = Y0 outside a circle, the image system consists of a counterclockwise image at the same image point as for the source and a clockwise vortex at the origin. Both of these image systems are illustrated in Fig. 6.24.

As a final example, take

which is the complex potential for a doublet of strength /л at Y = У0 whose axis is at an angle a to the x direction. With the use of the result that

and the complex potential for the doublet outside of a circle becomes

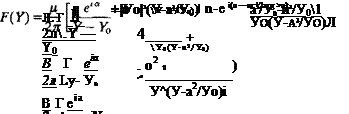The following manipulation will put the result in the form of a recognizable image system:

where the constant term has been neglected. The image of the doublet in a circle is therefore seen to be another doublet inside the circle at the image

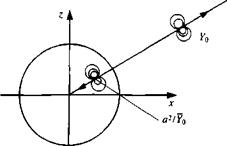FIGURE 6.25

Image of radial doublet outside a circle.

point previously derived for the source but with a reduced strength

For the special case of a doublet pointing outward along the radial line from the origin, arg Y0= a, and the complex potential becomes

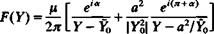(6.99)

This doublet plus its image are shown in Fig. 6.25.