PARAMETRIC ROBUSTNESS ANALYSIS

It is briefly illustrated that the /x tool, the x sensitivities (see subsec­tion 4.5 of chapter 1) and the skewed ц tool can be combined in order to maximize the stability domain of the closed loop in the space of a structured model perturbation: see (Ferreres and M’Saad, 1996) for an application to a missile example.

For the sake of clarity, let a closed loop subject to just two paramet­ric uncertainties 5i and <52. Figure 7.4 shows the stability domain in the space of (5i and <52, which correspond to normalized uncertainties in the stability derivatives Nr and Щ of a missile (Ferreres and M’Saad, 1996). The zero point corresponds to the nominal closed loop system, which is by assumption asymptotically stable. /z analysis provides the

largest square in the parameter space, inside which closed loop stability is guaranteed. The и tool however provides the largest rectangle in the parameter space, inside which closed loop stability is guaranteed.

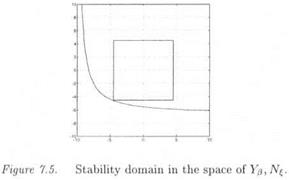
Nevertheless, the s. s.v. and the v measure can provide the same sta­bility domain, e. g. in the case of Figure 7.5 (81 and 82 now correspond to normalized uncertainties in the stability derivatives Y/3 and N ). In practice, p analysis is first applied. n sensitivities detect then whether the situation of Figure 7.4 or 7.5 is encountered. In the situation of Figure 7.4, the guaranteed domain of stability in the space of model uncertainties is further extended with the I’tool.