SECOND-ORDER SOLUTION

Consider the second-order solution. Define fictitious thickness and camber functions as

This puts the second-order problem in the same form as the first-order one at zero angle of attack (see boundary conditions in Eqs. (7.14)-(7.16)) and the

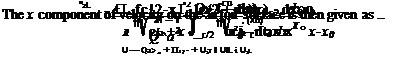solution can be written as

and the z component is obtained from the boundary conditions (Eqs. (7.15) and (7.16)).

The surface speed on the airfoil is the magnitude of the velocity and to obtain its value at any order the velocity components at that order are substituted into

q = Vm2 + w2 (7.24)

the expansion for the square root

(l+x)1/2 = 1 + — — +•• • for ДГ < 1

2 о

is used, the results are evaluated in terms of values on the chordline, and only terms up to the desired order are kept. The expressions for the surface speed correct to first and second order are derived as follows. On the surface, to second order,

, , 2 Гл/, Л ЗФ[ ЭФ212 Г ЭФ! ЭФ212

q=u+w =|q„(i-t)+_ + _J +^„a + _ + _j

If the results are evaluated at z = 0 and terms up to second order are kept,

ql = Ql + 2G»(u1T ± UiL + u2T ± u2L) + 2Q„r)

„ ЭФ, Г 9Фі І2

+ (uir ± ulLf + 26»*— (x, 0±) + 1^— (x, 0±)j

Note that

^Фі д ЗФі Э

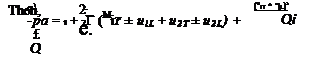0±) – 5-5*1<*•0±) – 0-5 – °-’1′

+ 2a(r)’ — a) + 2г)г)" + (ту’ – a)2

= 1 + ^- (Mlt ± Mil + u2T ± u2L) + (U’T – a2 + (ту’)2 + 2туту"

With the use of Eq. (7.24a) we get q2 If 2

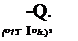~q~ = 1 + 2 Yq~ (UlT ^ UlL Urr ^ uil)

Therefore,

Q , Ut Mi#

— = і + —± —

CL Є. Є»

m±";>2-t ir25b)

The surface pressure coefficient (correct to second order) is obtained from Bernoulli’s equation as follows:

C =1-^

p Ql

Compare the expression for ql/Ql above to the expression for q2IQ^ in Eq. (7.25b) to observe that

and therefore

Qoo / VQoo Q,

The airfoil lift coefficient can then be determined from

1 (ca

C, = – [Cp(x, 0-) – Cp(x, 0+)] dx

C J-c/2

and with the use of Eqs. (7.25b) and (7.26) is

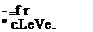4 ,U" Mq21L + 7P+ Wc + VcV’!+ Vcnl) dx (7.28)

To illustrate the results of second-order thin-airfoil theory, consider a symmetric airfoil at angle of attack and the surface speed is to be calculated. The following thickness function represents a symmetric Joukowski airfoil to second order in thickness ratio (see Van Dyke,5 3 p. 54):

where t, = 4т/ЗУЗ and r is the thickness ratio. To evaluate the Cauchy principal value integrals appearing in the equations for the x component of velocity at various orders, it will be advantageous to use Appendix A, which is
reproduced from Ref. 7.2. Therefore, lengths must be scaled by half the chord length to obtain the limits of integration from -1 to +1. Introduce the nondimensional coordinate x = x/(c/2). The nondimensional thickness func­tion for the Joukowski airfoil becomes

The nondimensional versions of Eqs. (7.17) and (7.19) for this symmetric airfoil become “ir 1 f1 df), dx о n = If – (*o) – – Qoо it J—і dx x – x0 (7.31a) “XL / 1-Х Qa “Vl+i (7.31ft) The slope of the nondimensional thickness function is ^~-‘= т,(1 – jc2)-U2(-1 —x + 2×2) (7.32) and the first-order x component of velocity becomes е_-1 + т,<1 (7.33) The nondimensional thickness and camber functions at second order (Eqs. (7.20a, ft)) are then

Vh = TiVl – Xі (1 – 3x + 2×2)	(7.34a)
»7c2=*1<*(1-*)2	(7.34ft)
and their nondimensional derivatives are
	(7.35a)
	(7.35ft)

The second-order result for the x component of velocity is obtained from the nondimensional version of Eqs. (7.21), (7.22), and (7.23) and is

The second-order result for the surface speed from Eq. (7.25b) is obtained with some manipulation as

FIGURE 7.2

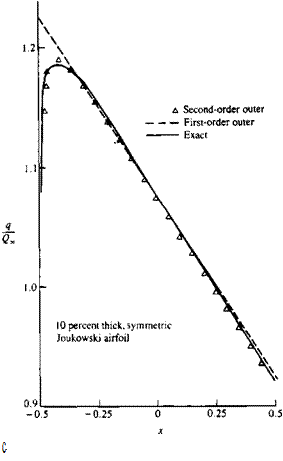Surface speed results for 10 per­cent thick symmetric Joukowski airfoil.

The first – and second-order surface speeds for a 10 percent thick Joukowski airfoil are shown in Fig. 7.2 and compared with the exact result from Chapter 6 for the case with zero angle of attack. It is noted that the first-order thickness solution is not singular at the leading edge but that the leading-edge stagnation point and the acceleration region following it are not predicted by the theory. This is not surprising since the approximations of the theory are invalid in the neighborhood of a stagnation point and round edge. The deceleration region over the rear of the airfoil appears to be predicted well by the theory. The second-order surface speed improves the comparison with the exact results over most of the foil (including the maximum speed) but is now singular at the leading edge. If we were to continue to higher order, the solution would become more and more singular at the leading edge and the thin-airfoil theory is not able to predict the correct behavior in this region.