Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
Some Properties of Three-Dimensional Attached Viscous Flow
To apply a simplification or an approximation makes only sense, if the real situation is sufficiently known. Therefore we consider now some properties of attached viscous flow, i. e., three-dimensional boundary layers. For a general introduction to three-dimensional attached viscous see [1]. No comprehensive description of separated and vortical flows is available. We refer the reader in this respect to, e. g., [2]-[5].
A three-dimensional boundary layer is governed by the two-dimensional external inviscid flow at or very close to the surface of the body. This external inviscid flow is two-dimensional in the sense that its streamlines are—to different degrees—curved tangentially to the body surface. As a consequence of this curvature locally all boundary-layer streamlines are stronger curved than the external streamline [1]. The skin-friction line, finally, thus can have quite another direction than the external inviscid streamline. In practice this means, that, for instance, the surface oil-flow pattern on a wind-tunnel model is not necessarily representative for the pattern of the external inviscid flow field close to surface.
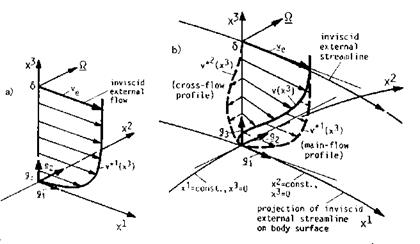
A stream surface, i. e., a boundary-layer profile, in a three-dimensional boundary layer defined in direction normal to the body surface, will become skewed in downstream direction due to the different curvatures of its streamlines. This is in contrast to a two-dimensional boundary layer, where the stream surface keeps its shape in the downstream direction. Hence the boundary layer profiles look different in the two cases, Fig. 7.1 a) and b).
If in a three-dimensional boundary layer on an arbitrary body surface the coordinate system locally is oriented at the external stream line, we call it a locally monoclinic orthogonal external-streamline oriented coordinate system [1].[85] In such a coordinate system the skewed boundary-layer profile can be decomposed into the main-flow profile and the cross-flow profile, Fig. 7.1 b). The main-flow profile resembles the two-dimensional profile, Fig. 7.1 a). The cross-flow profile by definition has zero velocity v*2 = 0 at both the surface, x3 = 0, and the boundary-layer edge, x3 = S.
|
Fig. 7.1. Wall-near viscous part of the stream surface, schematics of boundary- layer profiles [1]: a) two-dimensional flow (not skewed), b) three-dimensional flow (skewed). External inviscid streamline-oriented coordinate systems: x1 and x2 are the surface-tangential coordinates with v*1(x3) and v*2(x3) the related stream-wise (main-flow) and cross-flow viscous-flow profiles, x3 is the surface-normal coordinate. The resulting velocity profile in the 3-D case is v(x3). Q_ is the vector of vorticity content of the boundary layer [5]. |
The cross-flow profile, however, changes its shape, if the external inviscid streamline changes its curvature in the plane tangential to the body surface. Then an s-shaped profile will appear in the region just behind the inflection point of the external streamline, and finally an orientation of the profile in the opposite direction, Fig. 7.2.
