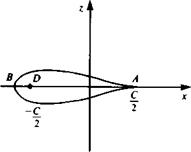
Symmetric Joukowski Airfoil

1

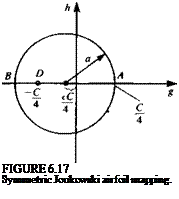
Let the center of the circle be taken on the real axis,

(x = – eC/4 €>0 (6.56)

so that from Eq. (6.27)

/3 = 0 a=^(l + e) (6.56a)

The circle is transformed into the airfoil shape shown in Fig. 6.17 (note that e should be small). The surface of the airfoil is given by (Eq. (6.24))

C2

єС C 4 +

= — [—e + (1 + e) cos в + i(l + б) sin 0]

Note that Y(-6) = У and therefore the resulting airfoil is symmetric. The chordlength c is given by

с = У(0 = О) + |У(0 = я)|=^{(1 + 2є)[і + ^-^]+2}

-£{3 + 2e + (TT2o) (6’58)

For small e, the chordlength is approximated by

c = j {3 + 2e + 1 – 2e + 4e2 + • • •} = C{ 1 + 4e2 + ■ ■ •} (6.59)

We can therefore take c = C. The velocity at the cusped trailing edge is given by Eq. (6.32) as

and the lift coefficient is (when C is the chord) given by Eq. (6.29a) as

С, = 2я(1 + e) sin a (6.61)

The thickness ratio is approximately equal to 1.299e.