The general theory for wings of high aspect ratio
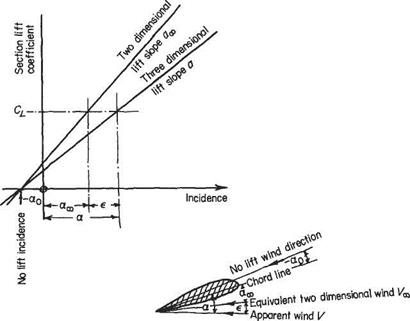
A start is made by considering the influence of the end effect, or downwash, on the lifting properties of an aerofoil section at some distance z from the centre-line of the wing. Figure 5.34 shows the lift-versus-incidence curve for an aerofoil section of
|
Cl = <3oo[«oo — c*o] = <з[а <*о] Taking the first equation with = a — є Cl = «ос [(a – ao) – <?] But equally from Eqn (4.10) lift per unit span / |
|
|
|
|
|
|
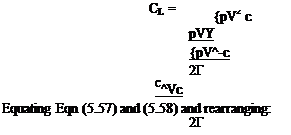 |
|
|
|
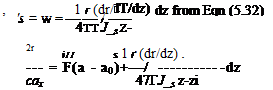 |
|
and since
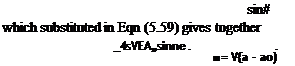
![]() This is Prandtl’s integral equation for the circulation Г at any section along the span in terms of all the aerofoil parameters. These will be discussed when Eqn (5.59) is reduced to a form more amenable to numerical solution. To do this the general series expression (5.45) for Г is taken:
This is Prandtl’s integral equation for the circulation Г at any section along the span in terms of all the aerofoil parameters. These will be discussed when Eqn (5.59) is reduced to a form more amenable to numerical solution. To do this the general series expression (5.45) for Г is taken:
r = 45F]T An sin пв The previous section gives Eqn (5.48):
VEnA„ sin пв
V Y nAn sin пв
cax ‘ ‘ sin в
Cancelling V and collecting cax/Bs into the single parameter ц this equation becomes:
ЭО
ц{а – a0) = J An sinn6»(l +^j)
Я=1
The solution of this equation cannot in general be found analytically for all points along the span, but only numerically at selected spanwise stations and at each end.