UNSTEADY MOTION OF A SLENDER WING

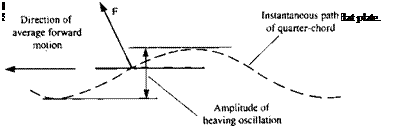
As the simplest example for the conversion of a three-dimensional wing theory to the time-dependent mode, consider the planar motion of a slender wing in the x, z plane.13 5 (This is a three degrees of freedom motion with X, Z, and в as shown in Fig. 13.21.) Since for a slender wing the longitudinal dimension is much larger than the other two dimensions (x »y, z) we can assume that the derivatives are inversely affected such that:

э_ д_ d_

Эх ^ dy ’ dz

As in the case of the steady-state flow over slender wings and bodies, substitution of this condition into the continuity equation (Eq. (13.12)) allows us to neglect the first term, compared to the other derivatives:

This suggests that the crossflow effect is dominant, and for any x = const, station, a local two-dimensional solution is sufficient. An interesting aspect of this simplification is that the wake influence is negligible, too, as long as the longitudinal time variations (e. g., wing’s forward acceleration) are small.

The slender, thin lifting surface with a chord length of c is shown schematically in Fig. 13.21. At t = 0 the wing is at rest in the inertial system X, Y, Z, and at f > 0 it moves along a time-dependent curved path, S (for this particular case S is assumed to be two-dimensional). For convenience, the coordinates x, z are selected such that the origin О is placed on the path 5, and the x coordinate is always tangent to the path. The wing shape (camberline) is given in this coordinate system by r/(x, t), which is considered to be small (jj/c«1, since small-disturbance motion is assumed). Also, the normal component of the kinematic velocity is small (e. g., ec/U(t) « 1).

The time-dependent version of the boundary condition requiring no normal flow across the surface (at any x = const, station) for this case is given by Eq. (13.50):

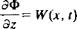
(13.77)

where Ф is the wing’s perturbation potential and the subscript В is not used for the slender wing case (since the wake effect is neglected).

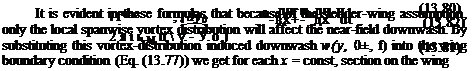and it is clear that y, U, rf, and в are functions of time. Comparing this form of the boundary condition with the formulation for high-aspect-ratio wings (Eq. (8.11)) clearly indicates that due to the slender-wing assumption the effect of the vortex lines parallel to the у axis (including the time-dependent portion of the wake) were neglected.