Validation
A series of calculations has been performed with the design and analysis codes in order to assess their capabilities and performances.
First, the analysis code has been used to predict the power captured by the NREL rotor for a range of TSR values and compare the theoretical results with the experimental measurements performed in the NASA Ames 80′ x 120′ wind tunnel [1]. The range in wind velocities is from 5 to 20m/s. The results are shown in Fig. 10.17, the large circles corresponding to the experiments and the small squares to the vortex model prediction. As can be seen, the model predicts the power coefficient accurately
|
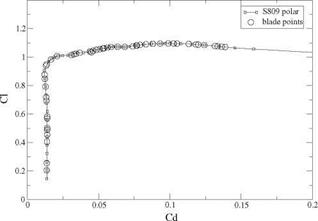
Fig. 10.15 Viscous polar at Re = 500,000 and blade working conditions at TSR = 3.8 |
|
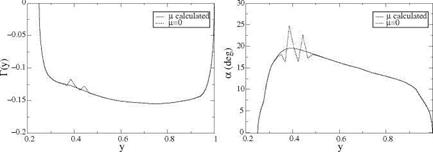
Fig. 10.16 Circulation and incidence distributions for the S809 blade at TSR = 3.8 |
for high TSR values, when the flow is attached, but for TSR < 3.3 much of the blade is stalled and the prediction becomes poor.
Secondly, for four values of the tip speed ratio, TSR = 2.9, 3.3, 3.8, 4.6, four rotors are designed with the optimization code each at the TSR and at the same CT coefficient corresponding to the value of the NREL rotor thrust on the tower. These results are shown as large squares in Fig. 10.17. In all cases the optimum rotor improves the power capture of the rotor by a significant amount. Then, for each of these rotors, the geometry has been kept fixed and the tip speed ratio varies to investigate off-design performance. The dotted lines in Fig. 10.17 show the results of this study. It is clear that the optimum rotor does not perform well at high TSR compared to the NREL rotor. However it must be noted that the power captured in that area is small and the benefit is really for low TSR’s, because the power increases proportionally to V3 and most of the energy resides in TSR < 3.3. It must be also
 |
0 1 2 3 4 5 6 7
TSR
Fig. 10.17 Optimum rotors and analysis comparison with NREL rotor noted that rotor blades have a variable pitch that can be used to compensate for the change in wind speed, a feature that has not been used in this study.
The analysis code performs well and is efficient and reliable when the flow is attached. This is consistent with the results obtained with the Prandtl lifting line theory applied to wings of large aspect ratios. When significant amount of separation occurs on a blade, the results are no longer accurate. The viscous effects tend to introduce strong blade-wise gradients that are not predictable with a 2-D viscous polar and strip theory. Attempts have been made at modifying the polar to account for these effects, using the experimental data as a guide, but the results remain limited to the particular rotor and wind velocity to which the viscous polar have been tuned. A more productive approach is the hybrid method, to be described later, which consists in using aNavier-Stokes solver to capture the viscous effects in the blade near field and the vortex model for the far field and boundary conditions of the Navier-Stokes code.