Viscous Correction

The viscous effects are considered a small deviation of the inviscid solution at the design point. In particular, the design lift distribution along the blade is such that Cl(y) < Clmax. The viscous torque and viscous thrust coefficients, CTv and CTv are added to their inviscid counterparts. For one blade

Ctv = – q(У) y – + w(y)) Cdvc(y)ydy (10.80)

n y0 adv >

1 Г1

Ctv = q(y)(1 + u(y)) Cdvc(y)dy

п У0

In discrete form

where the 2-D viscous drag coefficient, Cdvk, is approximated locally by a parabola [10]. The viscous polar, Ci versus Cdv is obtained from experimental measurements or numerical simulation, as a data set {Cdvm, Clm, am} where m is the index corre­sponding to the а-sweep. The viscous drag is locally given by

Cdv(Cl) = (Cd0)m + (Cd 1 )mCl + (Cd2)mCf (10.84)

The optimization proceeds along lines similar to the inviscid case. First an inviscid solution is obtained. Then the viscous correction is performed. к is defined as before, with Ct 1 replaced by Ct 1 + Ctv1, Ct2 by Ct2 + Ctv2 and CTtarget replaced by CTtarget – Ct0 and X reads

where the viscous contributions have been decomposed into 3 terms, independent, linear and quadratic functions of Г as

CTV = Ctv0 + Ctv1 + CTv2 (1°.86)

Ct v = Ct v0 + Ct v1 + Ct v2 (10.87)

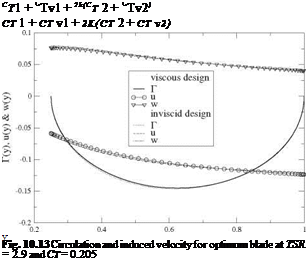
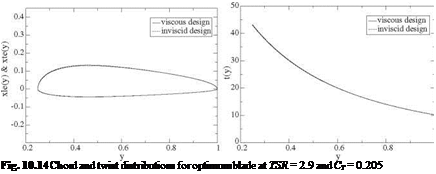
The inviscid and viscous distributions are compared in Figs. 10.13 and 10.14, for the TSR = 2.9 and CTtarget = 0.205. As can be seen, the effect of viscosity on the geometry is very small, however the efficiency drops 3.5% from n = 0.177 to П = 0.171.