6.3 Approximate Equations for the Longitudinal Modes 173

elegant result is not only of historical interest—it actually gives a reasonable approxi­mation to the phugoid period of rigid airplanes at speeds below the onset of signifi­cant compressibility effects. Thus for the B747 example, the Lanchester approxima­tion gives T = 107s, a value not very far from the true 93s. It is possible to get an even better approximation, one that gives an estimate of the damping as well. Be­cause q is approximately zero in this mode, we can infer that the pitching moment is approximately zero—that the airplane is in quasistatic pitch equilibrium during the motion. Moreover the pitching moment can reasonably be simplified in these circum­stances by keeping only the first two terms on the right side of (4.9,17e). Because q and w are both relatively small we further neglect Zq and as well. On making these simplifications to (4.9,18) and setting Af, = 0 and 6() = 0 we get the reduced system of equations:

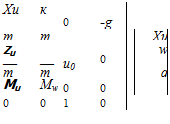
An

w

0

Afl

These equations are not in the canonical form x = Ax, but we can still get the charac­teristic equation by substituting x = x0eA’ and factoring out the exponential. The re­sult is

(Xu/m – A)	XJm	0	-g
ZJm	{ZJm – A)	n0	0
Mu	Mw	0	0
0	0	1	-A

Equation (6.3,7) expands to

АЛ2 + ВЛ + С = 0

or A2 + 2£w„A + w2n = 0 (6.3,8) which is a convenient way to write the characteristic equation of a second-order sys­tem. The constants are

A = ~u0Mw

В — gMu H {XUMW – MUXJ
m

c = – (zuMw – MUZJ m

from which we derive the radian frequency and damping to be

M, z

Table 4.4 with CZa = 0 is substituted into (6.3,12) we find (see Exer­cise 6.1) that Г„ = 1тгІ(оп is exactly the Lanchester period (6.3,5). Moreover if we make the further assumption that the airplane is a jet with constant thrust (dT/du0 = 0) we find the damping ratio to be that is, it is simply the inverse of the L/D ratio of the airplane. In fact the approxima­tion for the period is good over the whole range of Cmu, whereas that for the damping is poor for large positive Cmu. For the example airplane the above approximation gives t, = 0.066, compared with the exact value 0.049.

SHORT-PERIOD MODE

Figure 6.3b shows that the short-period mode is essentially one with two degrees of freedom, the speed being substantially constant while the airplane pitches relatively rapidly. We can therefore arrive at approximate system equations by neglecting the X-force equation entirely and putting Ди = 0. Examination of the magnitudes of the terms in the numerical example shows that is small compared to m and Zq is small compared to mu0. The result after simplifying (4.9,18) with в0 = 0 is a pair of equa­tions for w and q.

The characteristic equation of (6.3,13) is found to be

When converted with the aid of Tables 4.1 and 4.4, (6.3,14) becomes

A2 + BA + C = 0 (a)

В =—— t*

r*2/’

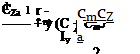where

When the data for the B747 is substituted into (6.3,15) the result obtained is

A2 + 0.741A + 0.9281 = 0 with roots A = —0.371 ± 0.889

which are seen to be almost the same as those in (6.2,3) obtained from the complete matrix equation. The short-period approximation is actually very good for a wide range of vehicle characteristics and flight conditions.