Approximate Solution Techniques

There are several popular methods that make use of a set of modes or other functions to approximate the dynamic behavior of systems. In this section, without going into detail about the theories associated with this subject, we illustrate within the framework already established how we can use a truncated set of modes or another set of functions to obtain an approximate solution. Details of the theories behind modal approximation methods are found in texts that treat structural dynamics at the graduate level. The two main approaches are (1) Galerkin’s method, applied to ordinary or partial differential equations; and (2) the Ritz method, applied to Lagrange’s equations or the principle of virtual work. These two methods yield identical results in certain situations. Thus, if time is limited, it would be necessary to discuss only one of the two methods to give students an introduction to the method and an appreciation of results that can be obtained this way. The Ritz method is preferred in the present context because of the ease with which it can be presented within the framework of Lagrange’s equations. Nevertheless, both of these methods are presented at a level suitable for undergraduate students.

3.5.1 The Ritz Method

Building on the previous treatment, we start with Lagrange’s equations, given by

where in the Lagrangean, L = K – P, the total kinetic energy is K, the total potential energy is P, n is the number of generalized coordinates retained, the generalized coordinates are ^, and Ei is the generalized force. Although it can be helpful, as discussed herein, it is not necessary to make use of potential energy, which can account only for conservative forces. The generalized force, however, can be used to include the effects of any loads. So as not to count the same physical effects more than once, the generalized force should include only those forces that are not accounted for in the potential energy. The generalized forces stem from virtual work, which can be written as

n

SW =J2 Eis& (3.295)

i =1

where S& is an arbitrary increment in the ith generalized coordinate.

Consider a beam in bending as an example. The total kinetic energy must include that of the beam as well as any attached particles or rigid bodies. The contribution

(3.296)

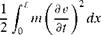
where m is the mass per unit length of the beam. The total potential energy P = U + V comprises the internal strain energy of the beam, denoted by U, plus any additional potential energy, V, attributed to gravity, springs attached to the beam, or applied static loads. All other loads, such as aerodynamic loads, damping, and follower forces, must be accounted for in Ei.

The strain energy for a beam in bending is given by

The expression for V varies depending on the problem being addressed, as does the virtual work of all forces other than those accounted for in V. The virtual work of an applied distributed force per unit length f (x, t) can be written as

SW = f f(x, t)8v(x, t)dx (3.298)

J0

where Sv is an increment of v in which time is held fixed and f (x, t) is positive in the direction of positive v.

To apply the Ritz method, we need to express P, K, and S W in terms of a series of functions with one or more terms. For a beam in bending, this means that

n

v(x, t) = J2 Si (t)Фі (x)

i=1

There are several characteristics that these “basis functions” фі must possess, as follows: [3] [4] [5]

Examples of complete sets of functions on the interval 0 < x < £ include

1, x, x2,…

. /П x (2nx . (3nx

sm( ~) ’ sm ~) ’ sin ~T

a set of mode shapes for any problem

Completeness also implies that there can be no missing terms between the lowest and highest terms used in any series.

4. The set of functions must be linearly independent. This means that

n

ai фі (x) = 0 ^ at = 0 for all і

i=0

A set of functions that satisfies all of these criteria is said to be “admissible.”

By use of the series approximation, we reduced a problem with an infinite number of degrees of freedom to one with n degrees of freedom. Instead of being governed by a partial differential equation, the behavior of this system is now defined by n second-order, ordinary differential equations in time. This reduction from a continuous system modeled by a partial differential equation with an infinite number of degrees of freedom to a system described by a finite number of ordinary differential equations in time is sometimes called spatial discretization. The number n is usually increased until convergence is obtained. (Note that if inertial forces are not considered so that the kinetic energy is identically zero, then a system described by an ordinary differential equation in a single spatial variable is reduced by the Ritz method to a system described by n algebraic equations.)

Now, let us illustrate how the approximating functions are actually used. Let фі, і = 1,2,…, ж, be a complete set of p-times differentiable, linearly independent functions that satisfy the displacement and rotation boundary conditions. Thus, U can be written as

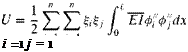(3.301)

The contributions of any springs that restrain the structure, as well as conservative loads, must be added to obtain the full potential energy P.

The kinetic energy of the beam is

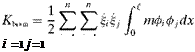(3.302)

Contributions of any additional particles and rigid bodies must be added to obtain the complete kinetic energy K.

The virtual work must account for distributed and concentrated forces resulting from all other sources, such as damping and aerodynamics. This can be written as

(3.303)

where x0 is a value of x at which a concentrated force is located. Here, the first term accounts for a distributed force f (x, t) on the interior of the beam, and the second term accounts for a concentrated force on the interior (see Eq. 3.96). In aeroelasticity, the loads f (x, t) and Fc(x0, t) may depend on the displacement in a complicated manner.

The integrands in these quantities all involve the basis functions and their deriva­tives over the length of the beam. Note that these integrals involve only known quan­tities and often can be evaluated analytically. Sometimes they are too complicated to undertake analytically, however, and they must be evaluated numerically. Numeri­cal evaluation is often facilitated by nondimensionalization. Symbolic computation tools such as MathematicaTM and MapleTM may be helpful in both situations.

With all such things considered, the equations of motion can be written in a form that is quite common; viz.

[M] {f} + [C] {1} + [K] (f } = {F}

where (f} is a column matrix of the generalized coordinates, {F} is a column matrix of the generalized force terms that do not depend on f, () is the time derivative of (), [M] is the mass matrix, [C] is the gyroscopic/damping matrix, and [K] is the stiffness matrix. The most important contribution to [M] is from the kinetic energy, and this contribution is symmetric. The most important contribution to [K] is from the strain energy of the structure and potential energy of any springs that restrain the motion of the structure. There can be contributions to all terms in the equations of motion from kinetic energy and virtual work. For example, there are contributions from kinetic energy to [C] and [K] when there is a rotating coordinate system. Damping makes contributions to [C] through the virtual work. Finally, because aerodynamic loads, in general, depend on the displacement and its time derivatives, aeroelastic analyses may contain terms in [M], [C], and [K] that stem from aerodynamic loads.

An interesting special case of this method occurs when the system is conser­vatively loaded. The resulting method is usually referred to as the Rayleigh-Ritz method, and many theorems can be proved about the convergence of approxima­tions to the natural frequency. Indeed, one of the most powerful of such theorems states that the approximate natural frequencies are always upper bounds; another states that adding more terms to a given series always lowers the approximate natural frequencies (i. e., making them closer to the exact values).

A further specialized case is the simplest approximation, in which only one term is used. Then, an approximate expression for the lowest natural frequency can be written as a ratio called the “Rayleigh quotient.” This simplest special case is of more than merely academic interest: It is not at all uncommon that a rough estimate of the lowest natural frequency is needed early in the design of flexible structures.

Example: The Ritz Method Using Clamped-Free Modes. In the first example, we consider a uniform, clamped-free beam that we modify by adding a tip mass of mass цті. The exact solution can be obtained easily for this modified problem using the methodology described previously. However, it is desired here to illustrate the Ritz method, and we already calculated the modes for a clamped-free beam (i. e., without a tip mass) in Section 3.3.4. These mode shapes are solutions of an eigenvalue problem; therefore, provided we do not omit any modes between the lowest and highest mode number that we use, this set is automatically complete. The set is also orthogonal and therefore linearly independent. Of course, these modes automatically satisfy the boundary conditions on displacement and rotation for our modified problem (because they are the same as for the clamped-free beam), and they are infinitely differentiable. Hence, they are admissible functions for the modified problem. Moreover, they satisfy the condition of zero moment at the free end, which is a boundary condition for our modified problem. However, because of the presence of the tip mass in the modified problem, the shear force—which readers will recall is proportional to the third derivative of the displacement—does not vanish as it does for clamped-free mode shapes.

The strain energy becomes

1 n n г

U = – £ J2 &&j ЕІф-ф’-dx (3.305)

2 t- j=i J°

Substituting the mode shapes of Eq. (3.258) into Eq. (3.305) and taking advantage of orthogonality, we can simplify it to

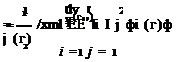where ai is the set of constants in Table 3.1. Similarly, accounting for the tip mass, the kinetic energy of which is

we obtain the total kinetic energy as

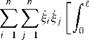(3.308)

With the use of the mode shapes in Eq. (3.258), we find that фі (г) = 2(-1)i+1; therefore, the kinetic energy simplifies to

i=1 j=1

Table 3.3. Approximate values of =■ for clamped-free beam with tip mass of ftml using n clamped-free modes of Section 3.3.4, Eq. (3.258) n lx = 1 ft = 10 Х = 100 1 1.57241 0.549109 0.175581 2 1.55964 0.542566 0.173398 3 1.55803 0.541748 0.173126 4 1.55761 0.541536 0.173055 5 1.55746 0.541458 0.173029 Exact 1.55730 0.541375 0.173001

where the Kronecker symbol Sij = lfori = j and Stj = Ofori = j. For free vibration, there are no additional forces. Thus, Lagrange’s equations now can be written in matrix form as

[M] {!} + [tf] {f} = 0 (3.310)

where [‘tf’] is a diagonal matrix with the diagonal elements given by

KH = Ellaf i = 1,2,…,n (3.311)

and [M] is a symmetric matrix with elements given by

Mij = ml [Sij + 4д(-1)+j ] i, j = 1, 2,…,n (3.312)

Assuming f = f exp(iat), we can write Eq. (3.310) as an eigenvalue problem of the form

[[tf] – m2[M]] {f} = 0 (3.313)

Results for the first modal frequency are shown in Table 3.3 and compared therein with the exact solution. As we can see, the approximate solution agrees with the exact solution to within engineering accuracy with only two terms. For contrast, results for the second modal frequency are shown in Table 3.4; these results are not nearly as accurate. Results for the higher modes (not shown) are even less accurate. This is one of the problems with modal-approximation methods; fortunately, however,

Table 3.4. Approximate values of?= for clamped-free beam with tip mass of p. ml using n clamped-free modes of Section 3.3.4, Eq. (3.258) n ft = 1 ft = 10 Х = 100 2 16.5580 15.8657 15.7867 3 16.3437 15.6191 15.5367 4 16.2902 15.5576 15.4744 5 16.2708 15.5353 15.4518 Exact 16.2501 15.5115 15.4277

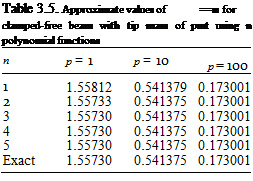aeroelasticians and structural dynamicists frequently are interested in only the lower – frequency modes. Note that the one-term approximation (i. e., the Rayleigh quotient) is within 1.1% for all values of p displayed.

Example: The Ritz Method Using a Simple Power Series. As an alternative to using the mode shapes of a closely related problem, let us repeat the previous solution using a simple power series to construct a series of functions Фі. Because the moment vanishes at the free end where x = t, we can make the second derivative of all terms proportional to t – x. To obtain a complete series, we can multiply this term by a complete power series 1, x, x2, and so on. Thus, we then may write the second derivative of the ith function as

(3.314)

With the boundary conditions on displacement and rotation being фі (0) = ф[ (0) = 0, we then can integrate to find an expression for the ith function as

Because the chosen admissible functions have nonzero third derivatives at the tip, they offer the possibility of satisfying the nonzero shear condition in combination with one another. Such admissible functions are sometimes called “quasi-comparison functions.”

In this case, the stiffness matrix becomes

and the mass matrix

Results from this calculation are given in Tables 3.5 and 3.6 for the first two modes. It is clear that these results are much better than those obtained with the

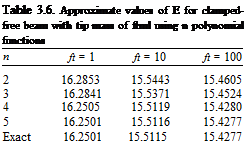clamped-free beam modes. It is not unusual for polynomial functions to provide better results than those obtained with beam mode shapes. However, here it is worth noting that the beam mode shapes are at a disadvantage for this problem. Unlike the problem being solved (and the polynomials chosen), the beam mode shapes are constrained to have zero shear force at the free end and thus are not quasi­comparison functions for the problem with a tip mass. This one-term polynomial approximation (i. e., the Rayleigh quotient) is within 0.05%, which is exceptionally good given its simplicity.

It is sometimes suggested that the mode shapes of a closely related problem are—at least, in some sense—superior to other approximate sets of functions. For example, in the first example, we saw that the orthogonality of the modes used re­sulted in a diagonal stiffness matrix, which provides a slight advantage in the ease of computing the eigenvalues. However, for the low-order problems of the sort we are discussing, that advantage is hardly noticeable. Indeed, symbolic computation tools such as MathematicaTM and MapleTM are capable of calculating the eigenvalues for problems of the size of this example in but a few seconds. Moreover, in some cases, the simplicity of carrying out the integrals that result in approximate formulations is a more important factor in deciding which set of functions to use in a standard im­plementation of the Ritz method. Indeed, polynomial functions are generally much easier to deal with analytically than free-vibration modes such as those illustrated in Section 3.5.1, which frequently involve transcendental functions.

Alternatives to the standard Ritz method include the methods of Galerkin, fi­nite elements, component mode synthesis, flexibility influence coefficients, methods of weighted residuals, collocation methods, and integral equation methods. We in­troduce Galerkin’s method and the finite element method in the next two sections. Detailed descriptions of other approaches are found in more advanced texts on structural dynamics and aeroelasticity.