Effect of altitude on power curves

We have not yet exhausted the information which can be obtained from these performance curves, for if we can estimate the corresponding curves for various heights above sea-level we shall be able to see how performance is affected at different altitudes. There is much to be said, and much has been said, on the subject of whether it is preferable to fly high or to fly low when travelling from one place to another. It is one of those many interesting prob­lems about flight to which no direct answer can be given, chiefly because there
are so many conflicting considerations which have to be taken into account. Some of them, such as the question of temperature, wind and the quantity of oxygen in the air, have already been mentioned when dealing with the atmos­phere, but the most important problem is that of performance.

How will the performance be affected as the altitude of flight is increased? Well, as the altitude increases, the air density decreases. Therefore, to support the same aircraft weight whilst maintaining the same lift coefficient and atti­tude, it is necessary to increase the speed so as to maintain the same dynamic pressure. What this means is that we need to fly at the same indicated air speed. This also means that the drag will remain the same as before. Thus, from the point of view of the airframe, it appears at first as though there is no disadvantage in flying high. Indeed we can actually fly faster for the same amount of drag and thrust. The main trouble with flying high though comes from the engine and propulsion system. The propulsion problems may be sum­marised as follows.

1. The power required is the product of the speed and the drag, so although the drag and thrust can remain the same when the height is increased, the increase in the speed means that the power required will increase.

2. The power output of piston engines falls as the air density reduces, and although we can compensate for this by adding a supercharger or tur­bocharger, there is a limit to the amount of supercharging that it is practical to use.

3. Since we need to fly faster to maintain the same lift and drag, the propeller will also have to go faster, and we will run into problems associated with compressible flow over the propeller.

In addition to these propulsion problems there are some other important airframe and operational considerations.

4. The cockpit and cabin need to be pressurised, which adds to the com­plexity and weight.

5. As the height and speed are progressively increased, we will eventually encounter the problems associated with compressibility, especially in respect of the propeller.

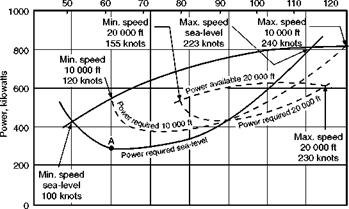
Whatever attempts are made to mitigate the difficulties of flight at high alti­tudes, in propeller-driven aircraft the general tendency remains for the power available to decrease and the power required to increase with the altitude (Fig. 7.4, overleaf). This will cause the curves to close in towards each other, resulting in a gradual increase in the minimum speed and a decrease in the maximum speed, while the distance between the curves, and therefore the rate of climb, will also become less. Any pilot will confirm that this is what actu­ally happens in practice, although, as previously mentioned, he may be

Fig 7.4 Effects of altitude

somewhat deceived by the fact that the air speed indicator is also affected by the change in density and consequently reads lower than the true air speed. This is really what accounts for the curve of power required moving over to the right as the altitude increases; if the curves were plotted against indicated speed, the curves for 3000 m and 6000 m would simply be displaced upwards, compared with that for sea-level. The difference between true and indicated speed also accounts for another apparent discrepancy in that the curves as plotted (against true speed) suggest that the air speed to give the best rate of climb increases with height. This is so, but the indicated speed for best rate of climb falls with height.

For certain purposes good performance at high altitudes may be of such importance that it becomes worth while to design the engine, propeller and aeroplane to give their best efficiencies at some specified height, such as 10 000 metres. It may then happen that performance at sea-level is inferior to that at the height for which the machine was designed. Even so, above a certain critical height, 6000, 9000 m or whatever it may be, performance will inevitably fall off and so the performance curves will be very similar, except that the highest curve of power available will correspond to the critical height. In such aircraft it may well be that the advantages of flying high outweigh the disadvantages.