EFFECT OF VERTICAL DENSITY GRADIENT

We might expect on physical grounds that the vertical gradient in atmospheric den­sity would have an effect on the phugoid mode. For when the airplane is at the bot­tom of a cycle and moving fastest it is also in air of greater density and hence would experience an additional increase in lift. It turns out that this effect is appreciable in magnitude. We shall therefore do two things: (1) show how to include this effect in the general equations of motion, and (2) derive a representative order of magnitude of the change in the phugoid period.

The modification to (4.9,18) consists of moving the Д zE equation into the matrix equation and adding some appropriate derivatives to the aerodynamic forces (4.9,17). Since the only possible steady reference state in a vertically stratified atmosphere is horizontal flight, we take 90 = 0. If A denotes the original system matrix, the result is

0 1 о

In (6.5,1) there are three new derivatives with respect to zE• Consider Zz first:

Z = CzpV2S

dZ dZ dp

= V[16]S

dZE Эр dzE

It is reasonable to neglect the variation of Cz with p, and the density varies exponen­tially with height,2 so that

p = p0eKZ£

and —— = кр (6.5,3)

uZe

where к is constant over a sufficient range of altitude for a linear analysis. It follows that

Xz — kX0 Mz = kM0

From (4.9,6) we get the reference values, leading to

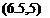
Zz = —mg к X=M= 0

The result is a rather simple elaboration of the original matrix equation. To get an es­timate of the order of magnitude of the density gradient effect, it is convenient to re­turn to the Lanchester approximation to the phugoid, and modify it to suit.

In Sec. 6.3 we saw that with this approximation, there is a vertical “spring stiff­ness” k given by (6.3,3) that governs the period. When the density varies there is a second “stiffness” k’ resulting from the fact that the increased density when the vehi­cle is below its reference altitude increases the lift, and vice versa. This incremental lift associated with a density change is

ДІ = ClV2S Дp

so that

Using (6.5,3) we get

k’ = kW

Thus we find that k’ is approximately constant, whereas k from (6.3,3) depends on CWoP, which varies as V~2 for constant weight. The density gradient therefore has its greatest relative effect at high speed. The correction factor for the period, which varies inversely as the square root of the stiffness, is

k y/2 1

k + k’j ~ (1 + k’/k)U2

so that the period, when there is a density gradient, is T’ = FT. With the given values of k and k’ this becomes

1

F = / kMq i/2 (6.5,8)

V 2SI

in which the principal variable is seen to be the speed. Using a representative value for к of 4.2 X 1СГ5 (6.5,8) gives a reduction in the phugoid period of 18% for the ex­ample airplane at 774 fps. This is seen to be a very substantial effect. If the full sys-

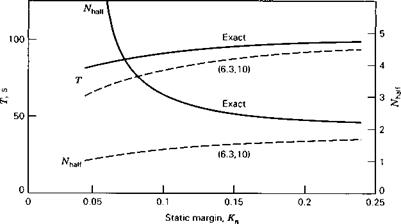
Figure 6.7 Variation of period and damping of phugoid mode with static margin.

tern model (6.5,1) is used, comparable effects can be found on the damping of the phugoid as well.