FLIGHT PATHS IN THE CHARACTERISTIC MODES

Additional insight into the modes is gained by studying the flight path. With the at­mosphere at rest, the differential equations for the position of the CG in FE are given by (4.9,10), with 0o = 0, that is,

Axe = A и A zE = ~uo0 + w

In a characteristic oscillatory mode with eigenvalues A, A*, the variations of Au, 0, and w are [cf. (6.1,8)]

Au = uXjekt + u*jeK ‘

w = u2jeM + u*je* ‘ (6.2,5)

0 = u4jex‘ + u*4jeK ‘

where the constants utj are the components of the eigenvector corresponding to A. For the previous numerical example, they are the complex numbers given in polar form in Table 6.4. After substituting (6.2,5) in (6.2,4) and integrating from t = 0 to t we get

$

U1 у U : *

XE — u0t H—– – eXt Л—– – ex 1 + const

E 0 A A*

eia*

(6.2,6)

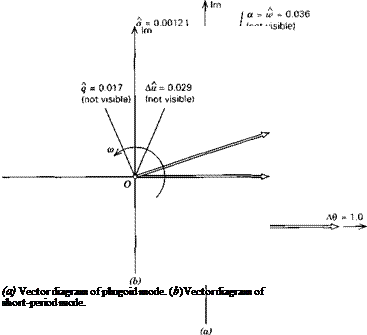Figure 6.3

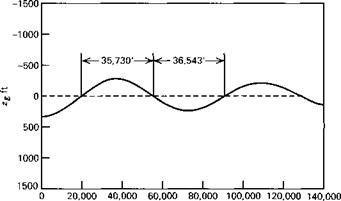
where Re denotes the real part of the complex number in the square brackets. For the numerical data of the above example (6.2,6) has been used to calculate the flight paths in the two modes, plotted in Fig. 6.4. The nonzero initial conditions are arbi­trary, and the trajectories for both modes asymptote to the steady reference flight path. Figure 6.4 shows that the phugoid is an undulating flight of very long wave­length. The mode diagram, Fig. 6.3a shows that the speed leads the pitch angle by about 90°, from which we can infer that и is largest near the bottom of the wave and least near the top. This variation in speed results in different distances being traversed

xE ft (a)

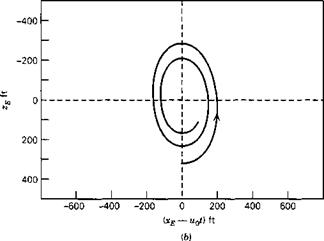
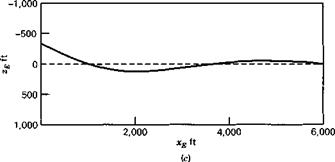
Figure 6.4 (a) Phugoid flight path (fixed reference frame), (b) Phugoid flight path (moving reference frame), (c) Short-period flight path.

during the upper and lower halves of the cycle, as shown in Fig. 6.4a. For larger am­plitude oscillations, this lack of symmetry in the oscillation becomes much more pro­nounced (although the linear theory then fails to describe it accurately) until ulti­mately the upper part becomes first a cusp and then a loop (see Miele, 1962, p. 273). The motion (see Sec. 6.3) is approximately one of constant total energy, the rising and falling corresponding to an exchange between kinetic and potential energy. Fig­ure 6Ab shows the phugoid motion relative to axes moving at the reference speed u0. This is the relative path that would be seen by an observer flying alongside at speed Mo-

Figure 6.4c shows the path for the short-period mode. The disturbance is rapidly damped. The transient has virtually disappeared within 3000 ft of flight, even though the initial Да and Ав were very large. The deviation of the path from a straight line is small, the principal feature of the motion being the rapid rotation in pitch.