Galerkin’s Method

Rather than making use of energy and Lagrange’s equation as in the Ritz method, Galerkin’s method starts with the partial differential equation of motion. Let us denote this equation by

£[v(x, t)] = 0

where L is an operator on the unknown function v(x, t) with maximum spatial partial derivatives of the order q. For the structural dynamics problems addressed so far, the operator L is linear and q = 2p, where p is the maximum order of spatial partial derivative in the Lagrangean. It is important to note, however, that it is not true, in general, that q = 2p; indeed, we do not need to consider the Lagrangean at all with this method.

To apply Galerkin’s method, we need to express v(x, t) and, hence, the operator L in terms of a series of functions with one or more terms. For a beam in bending, for example, this means that, as before

n

v(x, t) = ^21 j(t )ф j(x) (3.319)

j=i

Relative to the basis functions used in the Ritz method, the characteristics that these functions фі must possess for use in Galerkin’s method are more stringent, as follows:

1. Each function must satisfy all boundary conditions. Note that it is not easy, in general, to find functions that satisfy all boundary conditions.

2. Each function must be at least q times differentiable. The qth derivative of at least one function must be nonzero.

3. If more than one function is used, they must be chosen from a set of functions that is complete.

4. The set of functions must be linearly independent.

Functions that satisfy all of these criteria are said to be “comparison functions.” The original partial differential equation then is multiplied by фі and integrated over the domain of the independent variable (e. g., 0 < x < £). Thus, a set of n ordinary differential equations is obtained from the original partial differential equation. (Note that if the original equation is an ordinary differential equation in x, then Galerkin’s method yields n algebraic equations.)

Consider a beam in bending as an example. The equation of motion can be written as in Eq. (3.194), with a slight change, as

where EI is the flexural rigidity, m is the mass per unit length, and the boundary conditions and loading term f (x, t) must reflect any attached particles or rigid bodies. In aeroelasticity, the loads f (x, t) may depend on the displacement in a complicated manner.

With all of the components as described herein considered, the discretized equa­tions of motion can be written in the same form as in the Ritz method; that is

[M] {|} + [C] {|} + [K] {£} = {F} (3.321)

where {|} is a column matrix of the generalized coordinates, {F} is a column matrix of the generalized force terms that do not depend on I, ( ) is the time derivative of (), [M] is the mass matrix, [C] is the gyroscopic/damping matrix, and [K] is the

stiffness matrix. As before, inertial forces contribute to [M], there are contributions from the inertial forces to [C] and [K] when there is a rotating coordinate system, and damping also contributes to [C]. Finally, because aeroelastic loads, in general, depend on the displacement and its time derivatives, aerodynamics can contribute terms to [M], [C], and [K].

Example: Galerkin’s Method for a Beam in Bending. Now, we illustrate how the approximating functions are actually used. Let фі, i = 1,2,…, ж be a complete set of q-times differentiable, linearly independent functions that satisfy all of the boundary conditions. Substituting Eq. (3.319) into Eq. (3.320), multiplying by фі (x), and integrating over x from 0 to I, we obtain

j (ЕЩ У’ + ^ і тф j
dx = 0 і = 1, 2,…,n
(3.322)
f(x t)
j=i	j=i

After reversing the order of integration and summation and integrating the first term by parts, and taking into account that the functions фі satisfy all the boundary conditions, this equation becomes

dx = 0 і = 1, 2,…,n

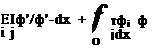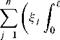
(3.323)

When we compare the first two terms with the previous derivation by the Ritz method, we see the close relationship between these approaches. Indeed, if the starting partial differential equation is derivable from energy—which implies that q = 2p—and the same approximating functions фі are used in both cases, the result­ing discretized equations are the same.

Considering the clamped-free case, for example, we can develop a set of com­parison functions by starting with

(3.324)

фі

With the boundary conditions on displacement and rotation being фі (0) = ф/(0) = 0, we then can integrate to find an expression for the rth function as

	6+і 2(1 – x)2+і
(3.325)
фі
і (1 + і )(2 + і )(3 + і)

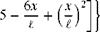
Elements of the stiffness matrix are found as

K = f ЕІф-ф’-dx

0

24 ЕІ

^3 (і + І — 1) (і + І) (1 +і + j) (2 +і + j) (3 + і + j)

Similarly, the elements of the mass matrix are found as

fг

Mij = m4i ф jdx

J0

m£p1

p2

where

p1 = 30,240 + 28,512(i + j) + 9,672(i2 + j2) + 1,392(i3 + j3) + 72(i4 + j4)

+ 20,040ij + 4,520(i2 j + ij2) + 320(i3 j + ij3) + 520i2 j2 p2 = i (1 + i)(2 + i)(3 + i) j(1 + j)(2 + j)(3 + j)(3 + i + j)

(4 + i + j )(5 + i + j )(6 + i + j )(7 + i + j)

(3.328)

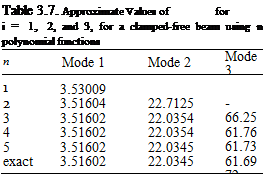
The fact that the governing equation is derivable from energy is reflected in the symmetry of [M] and [K]. Results for free vibration (i. e., with f = 0) are given in Table 3.7. As with the Ritz method, we see monotonic convergence from above and accuracy comparable to that achieved via the Ritz method. However, unlike the Ritz method, we do not always obtain results for free-vibration problems that converge from above.

Example: Galerkin’s Method for a Beam in Bending Using an Alternative Form of the Equation of Motion. Consider again a clamped-free beam. To obtain an alternative equation of motion, we integrate the equation of motion twice and use the boundary conditions of zero shear and bending moment to obtain an integro – partial differential equation

where z is a dummy variable. Although this equation of motion is somewhat more complicated, it is only a second-order equation. Thus, it has only two boundary conditions, which are zero displacement and slope at x = 0. Thus, a much simpler

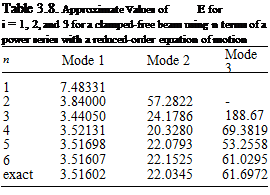
set of comparison functions can be used, such as a simple power series; that is

Фі = (-) i = 1,2,…,n (3.330)

We should not expect greater accuracy from this simple set of functions, but the analytical effort is considerably less. Indeed, the elements of the stiffness matrix are

Kij = f БІфі Ф"dx J0

EIj( j +1) t(i +j +1)

and the elements of the mass matrix are

p t p t

Mij = ф, (Z – х^фj (Z )dZ dx

J0 Jx

mt3

(2 +i )(3 + i )(5 + i + j)

Note that these matrices are not symmetric. Moreover, the results presented in Table 3.8 are not as accurate as those obtained in Table 3.7, and the convergence is not monotonic from above.

The partial differential equations derived previously for free vibration of strings, beams in torsion, and beams in bending can be derived from energy-based ap­proaches, such as Hamilton’s principle. (The use of Hamilton’s principle is beyond the scope of this text, but detailed treatments are found in numerous graduate-level texts on structural dynamics.) In those cases, the Ritz and Galerkin’s methods give the same results when used with the same approximating functions. As shown here, however, Galerkin’s method provides a viable alternative to the Ritz method in cases where the equations of motion are not of the form presented previously in this chapter.

Figure 3.44. Schematic of a nonuniform beam with distributed twisting moment per unit length