General Application of the Indicial Response Method

As described previously, if the indicial aerodynamic response(s) can be determined, then these solutions form a powerful means of finding the unsteady aerodynamic forces and pitching moments in the time domain in response to arbitrary variations in AoA and/or in­flow velocity by using Duhamel superposition. The effects of a time-varying incident flow
velocity may also be handled by means of this approach. There are two main difficulties with this method, however. The first is to determine the indicial response functions themselves. While they are known exactly for incompressible flow (e. g., Wagner and Kiissner func­tions), they are not known exactly for subsonic compressible flow. Nevertheless, there are various techniques that can be used to find and approximate forms of the indicial response from aerodynamic transfer functions obtained from experimental measurements. Second, numerical methods must be devised to enable the superposition process to be conducted accurately and computationally efficiently.

The indicial method is based on the fundamental principle that the flow can be linearized with respect to the forcing function. For example, a generalized unsteady force coefficient acting on the airfoil, say Cf(t), can be assumed to be a smooth, nonlinear function of angle of attack, a. About some mean value of angle of attack, say am, this allows C/ to be expressed as the first-order Taylor series expansion

This approximation will become more exact as the step Да -» 0. If С/ is a linear function of a, then Eq. 8.70 is already exact. If dCf/da is a linear time invariant response such that it does not depend on a and so depends only on the time after the step input is applied, then the linear result for С/ is

Cf(t) = Cf{t = 0) + ^-(t)Aa = Cf(t = 0) + 0/(0 Да, (8.71)

where 0/(0 is called the Umar indicial response of C/, in this case to a step input in a.

For arbitrary inputs in a, then as shown previously the value of С/ can then be expressed in terms of the Duhamel superposition (or convolution) integral as

dC f dC f da

Cf{t) = -^a(O)0y(O +-^-Jo ~ (8-72)

where the first term is a short time transient. The evaluation of the Duhamel integral, there­fore, produces an aerodynamic quantity that contains all of the prior time-history information of what has happened to the aerodynamic response since the initial time. Equation 8.72 is solved numerically (see Section 8.14.1) and different approaches can be formulated. Notice that in the limit of steady flow, Eq. 8.72 reduces to the trivial result that

(8.73)

which is fully consistent with linearized, steady airfoil theory.

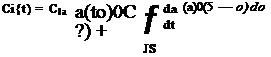The time-varying value of the lift coefficient, Q(t), can be expressed as a function of angle of attack, a(t), in terms of the Duhamel integral as

where 0(5) is indicial response to a unit step input a and Qa is the lift-curve-slope (= 27r/radian for incompressible flow). If the integral is evaluated, then the term ae(t) can be
viewed as an effective AoA in that it contains all the time history information.7 Equation 8.74 is usually solved numerically for discrete values of time. For a discretely sampled system at times s = s, ai, …. ,ct2,g, s, then ae(s) can be written using Eq. 8.74 as

^da

ae(s) = a(s0)cp(s) + 2_j — (о’іЖ’*’ – о^Да,-

(=i

= сфоЖ^) + ot'(a)4>(s – <7і)Д(7і + a'(a2)f(s – a2)Aa2 H——

4- a/(crl)0(5 – сг^Дсг,- H—– , (8.75)

with the summation extending over all inputs that have acted up to the instant 5. Therefore, the result for ae(s) requires the storage of a’Cs), afcrj),…, a'(oi) at all previous time steps and the repeated reevaluation of the indicial function for each 5 — cr, at each new time step. Obviously, in most cases information at a large number of previous time steps must be retained. Also, the indicial response function is not always known in a convenient simple analytic form, such as with the Wagner and Ktissner functions, so a relatively large number of numerical operations must be performed. This is not helpful for a helicopter rotor calculation, but, fortunately, there are alternative approaches to solving this numerical problem.