General Theory of Static Longitudinal Stability

In Chap. 2 we used positive pitch stiffness (negative CmJ as an approximate criterion for static longitudinal stability. Now static instability really means the presence of a real positive root of the characteristic equation, and we saw in Sec. 6.1 that the condi­tion for no such root to occur is that the coefficient E of the stability quartic must be positive. Thus the boundary between static stability and instability is defined by E = 0. We get E by putting A = 0 in the characteristic determinant. Thus

£ = det A (6.4,1)

In evaluating (6.4,1) for the matrix of (4.9,18) we put в0 = 0, and as in Sec. 6.3, we neglect the two derivatives Z,;. and Zq. The result is

E = – y (ZUMW – M Zw) (6.4,2)

mly

Since g, m and Iy are all positive, the criterion for static stability is

ZUMW – MUZW > 0. (6.4,3)

When converted to nondimensional form, this becomes

Cma(CZu – 2CWo) – CmCZa > 0 (6.4,4)

When there are no speed effects, that is, CZu and Cmu are both zero, then the criterion does indeed reduce to the simple Cm<x < 0.

We now compare the above criterion for stability with the trim slope (2.4,24). In making this comparison, we must take note of a minor difference in basic assump­tions. In the preceding development, it was specifically assumed that the thrust vector rotates with the vehicle when a is changed [see (5.1,1)]. In the development leading

to (2.4,24) by contrast, there is an implicit assumption that the thrust provides no component of force perpendicular to V [see (2.4,18)]. It is this difference that leads to the presence of CZa in (6.4,4) instead of CLa in (2.4,24). Had the assumptions been the same, the expressions would be strictly compatible. In any case, CDo is usually small compared to CLa, so that the difference is not important, see Table 5.1. We see that the justification for the statement made in Sec. 2.4, that the slope of the elevator trim curve (dSettim/dV)Sp is a criterion of static stability, is provided by (6.4,4). [Note that CWo = (6.4,4).]

Another stability criterion referred to in Chap. 2 is the derivative dCJdCL (2.3,8). It was pointed out there that this derivative can only be said to exist if enough constraints are imposed on the independent variables a, V, Se, q, etc., on which Cm and CL separately depend. Such a situation results if we postulate that the vehicle is in rectilinear motion (q = 0) at constant elevator angle and throttle setting, with L = W, but with varying speed and angle of attack. Such a condition cannot, of course, actually occur in flight because the pitching moment could be zero at only one speed, but it can readily be simulated in a wind tunnel where the model is restrained by a balance. With the above stipulations, Cm and C, reduce to functions of the two vari­ables u and a, and incremental changes from a reference state ( )0 are given by

dC, = C, da + C, dii dCm = Cma da + Cmu da

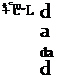The required derivative is then

provided dd/da exists. This is guaranteed by the remaining condition imposed, that is, L = W (implying aT = 0). For then we have

W = CL{a, ii)pV2S = const

from which we readily derive

(CLa da + CLu du)hpulS + CLiipu0S du = 0 (6.4,7)

From (6.4,7)

(CLu + 2CLo) da + CLa da = 0

da c,

___ __ c-a____

da CLu + 2CLo

After substituting (6.4,8) into (6.4,6) and simplifying we get

On comparing (6.4,9) with (6.4,4), with the same caveats as for the trim slope, we see that the static stability criterion is
provided that dCJdCL is calculated with the constraints A8e = A8p = q = 0 and L = W. [The quantity on the left side of (6.4,9) is sometimes referred to as speed stability in the USA, by contrast with “angle of attack” stability. In Great Britain, this term usually has a different meaning, as in Sec. 8.5.]

On using the definition of hs given in (2.4,26) we find from (6.4,9) that

(6.4,11)

that is, that it is proportional to the “stability margin,” and when CLu < 2CL:, is equal to it.