MATCHED ASYMPTOTIC EXPANSIONS

We will use the method of matched asymptotic expansions to obtain a solution that is uniformly valid over the airfoil surface. Our results will be presented essentially in outline form and further details are available in Van Dyke.5 3 The success of the method is predicated on the observation that the two solutions complement each other and it is expected that in the limits of their applicability they approach each other (the limit of the thin-airfoil solution as the leading edge is approached should somehow be equivalent to the limit of the local solution as the distance from the leading edge is increased). The local solution is called the inner solution and the thin-airfoil solution is called the outer solution.

The formal task of matching the inner and outer solutions is achieved through the asymptotic matching principle (Van Dyke,5 3 p. 90):

The m-term inner expansion of the л-term outer expansion = the л-term outer expansion of the лі-term inner expansion

Outer variables are scaled with the airfoil chord and inner variables are scaled with the nose radius; m and n are integers, not necessarily equal. The definition of the m-term inner expansion of the n-term outer expansion is expressed in the following sequence of steps:

1. Re-write the л-term outer expansion in inner variables.

2. Expand in an asymptotic series for small є (or r).

3. Keep m terms.

We will apply the above matching technique to the surface speed for the flow past a symmetric Joukowski airfoil at zero angle of attack. The three-term (я = 3) outer expansion in dimensionless coordinates is given in Eq. (7.37) as

£-l + rl(l-2f)-|£j<l + 2«)’ (7.47)

In terms of s = 2s/с = x + 1, Eq. (7.47) becomes

q = G-[ 1 + *i(3 – 2s) ~ (2s – l)2] (7.47a)

To second order in the thickness x, the airfoil can be represented locally by the parabola so that the two-term (m = 2) inner expansion is given in Eq. (7.46) as

The Joukowski airfoil (Eq. (7.30)) becomes

z = ± r,(2 – s)y/2s – s2 (7.49)

and as s —»0 we get the parabola z = ±V8t? s. From Eq. (7.40), the parabola is z = ±V4sr/c. The nose radius is therefore r = 2cx.

Let us now do the matching for q.

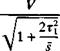Two term inner expansion (already in outer variables):

expanded for small

F(l-|) + 0(rt)

Three-term outer expansion:

F(l-|) (7.50c)

Three-term outer expansion:

e»[l + T1(3-2f)-^^(2s-l)2] (7.51a)

rewritten in inner variables (note that S = s/tf)

Q 1 + r,(3 -2r25) ~Y~^(2riS – l)2] (7.51b)

expanded for small r,

еф + З^-^ + О^2) (7.51c)

Two-term inner expansion:

Q”[1_J + 3Tl] = Є“[1 + ЗТі_1І] (7.51d)

The matching is complete when we equate the results for q from Eqs. (7.50c) and (7.51d) to get V — Q^(l + 3tj). The local solution therefore experiences a free-stream speed that is larger than the actual one.

The final step in the analysis is to combine the inner and outer solutions to obtain a solution valid over the complete airfoil surface. At best the solution will be as accurate as either the inner or outer expansions in their regions of applicability. The combined solution is called a composite expansion (Van

Dyke,5 3 pp. 94-97) and we will use the additive composite

f(m, n) = f(m) + fin) _ Ш = 2, П —3 (7.52)

The additive composite expansion is the sum of the inner and outer expansions minus the part they have in common (i refers to inner and о refers to outer). This common part, the last term in Eq. (7.52), is obtained during the matching process and is given in Eq. (7.50c). Our result is

J„-d + 3l’)Vl + 2tf 1 1 ‘ tl<3_ 2t)“ 2 Ї <b ‘>	І + Зг.-Ь]
	(7.53)
After some manipulations this result becomes
Gm-(1 + 3Ti)Vs + 2t? ^’2(^ 3)	(7.53«)

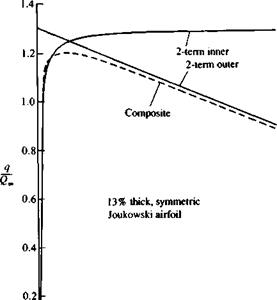
The important feature to note in the solution is that the singular part of the thin-airfoil result in the neighborhood of the leading edge has been removed. (Figure 7.5 compares the inner, outer and composite expansions for a particular value of the thickness.)

0І_______ I_______ I_______ I_______ I -0.5 – 0.25 0 0.25 0.5

FIGURE 7.5

Inner, outer, and composite ex­pansions for the 13 percent thick symmetric Joukowski airfoil.