MISSILE DYNAMIC EQUATIONS

As in the case of aircraft, the axis system for missiles for the development of EOM is also assumed to be centered at the CG and fixed to the body. Figure 3.13 shows the X, Y, and Z axes, which are also the roll, pitch, and yaw axes, respectively. The XY plane represents the yaw plane while the XZ plane is the pitch plane. The angle of incidence in the XZ plane is a, the sideslip angle in the yaw plane is b, and the ay in Figure 3.12 denotes the flank angle. After a few simple algebraic calculations, the following relation can be easily obtained from Figure 3.13:

tan b = tan ay cos a (3.31)

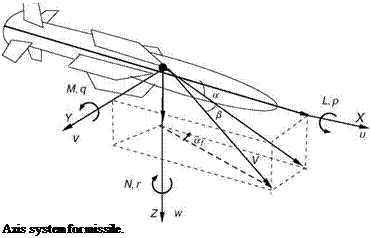и, v, and w are the velocity components in the body axis. Compared to v and w, the component u is much larger and varies little during the flight. Like the aircraft, the missile too has 6DOF motion, which is represented by three forces and three moment equations [8]. The standard set of equations normally used to compute missile dynamics is similar to Equations 3.11 and 3.15

FIGURE 3.13

Fx = m(ii + qw — rv)

Fy = m(v + ru) (3.32)

Fz = m(W — qu)

L = pIx — qlxy — rlxz + qr(Iz — Iy) + (r2 — q2)Iyz — pqlxz + rpIxy M = – pixy + qly — rlyz + rp(Ix — Iz) + (p2 — r2)Ixz — qrIxy + pqlyz (3.33)

N = —pixz — qiyz + riz + pq(Iy — Ix) + (q2 — p2)Ixy — rpIyz + qrixz

The FX equation includes i, which represents the change in the forward speed. To

compute this, we need to know the drag force and the thrust force acting on the missile. Since w and v are generally small, the contribution of the terms pw and pv in equations for FY and FZ will be small if and only if the roll rate is small. From another perspective, the rolling motion will cause forces in pitch and yaw plane, a feature that is highly undesirable and should be dealt with at the design stage. The undesirable effects of high roll rate may also be reduced using acceleration feedback from autopilot during the flight.

If the roll rate p is assumed to be small and the flight variables q, r, v, and w being small, EOM for the missile can be simplified by neglecting the terms involving the products of these variables, e. g., terms like pv, pw, pq, and pr. In addition, assuming the missile to be reasonably symmetrical about the XZ and XY planes, the simplified set of equations can be written as

Fx = m(u + qw — rv)

Fy = m(v + ru)

Fz = m(w — qu)

L = p Ix

M = qIy

N = rIz

The rolling moment equation here shows no coupling between the roll and pitch motions and the roll and yaw motions.