PITCH DAMPING OF PROPULSIVE JETS

When gases flow at high velocity inside jet or rocket engines, there is a consequent rate of change of moment of inertia which leads to an inertia term in the moment equation [<#выв in (5.6,7)]. Instead of retaining it as a term on the r. h.s., it is convenient to transpose it to the l. h.s. and treat it as an external moment AGB = —JGB*s>Pi. Considering only pitching motion,

"O’

g.

the corresponding terms in the scalar moment equations (5.6,8) are

A£ = Іхуі

Ш = – lyq (7.9,16)

= lyzq

The corresponding q derivatives are therefore

A Lq = txy

ЬМв = -4 (7.9,17)

A^ « = 1„

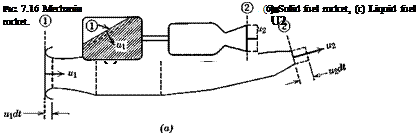
We restrict ourselves to consideration only of propulsion systems that have inertial symmetry with respect to the xz plane, so Ixy = Ivz = 0, and only ДЖв remains. Figure 7.16 shows three types of propulsion system, for each

of which we assume that the velocities are uniform across surfaces 1 and 2. For the jet engine 1 is the air inlet and for the rockets it is the moving boundary of the fuel. u2 is the jet exit velocity, щ is the inlet velocity for the jet, and the rate of movement of the relevant interface for the rockets.

The Oxz coordiate system of Fig. 7.16 is taken fixed to the solid part of the vehicle, and we focus our attention on the material system comprising the solid, liquid, and gaseous constituents of the vehicle at time zero. The boundaries of this system move in a time dt as illustrated; as a result its mass center moves away from the origin 0, and its moment of inertia changes. Let Iy be the moment of inertia around 0, and I’v be that around the displaced mass center, at coordinates (x, z). By the parallel axis theorem for moment of inertia we have

I’v = Iy — m(x2 + z2)

where m is, of course, the total vehicle mass. It follows that

ly = ly — 2m(x — + z

dt dt)

and at t = 0, when x — z = 0, І’у — ly. Thus the movement of the mass center associated with the jet flow does not contribute to the jet damping effect explicitly. The change in Iy in time dt is given by

dly — dt Г p%u2{x2 + z22) dA2 — dt f piU^x^2 + %i) (7.9,18)

JAz Ja і

In the second term, for a jet engine, px is, of course, the density of the inlet air. For a rocket it is, strictly speaking, the difference in density between the fuel and the adjacent gas. For all practical purposes the latter can clearly be neglected. If x2 and z2 are the component mean-square distances to the surfaces Ax and A2, (7.9,18) can be expressed as

iy = p2u2A2(x22 + z22) — pju^ixj2 + zx2) (7.9,19)

Now р(и{А( is the mass flux across A, h and may be taken constant for all three types of system (the fuel mass flow in jet engines is much smaller than the air mass flow). Thus

ly = m'[(x22 — Xj2) + (z2 — Zj2)] (7.9,20)

where m’ = А^щ is the mass flow rate out of the jet. In many practical cases, for elongated slender vehicles, the z2 terms may be negligibly small. The result for the pitch damping in that case is

It will be negative, corresponding to positive damping, whenever the C. G. is closer to the inlet or the fuel surface than to the nozzle exit. For compactness we may write f2 for (x22 — aq2) + (z22 — z,2) so that

Д Ma = – m’k2 (7.9,22)

The nondimensional coefficient follows as

It varies inversely as speed for constant propulsive mass flow m!. The thrust of the engine is given by

T — m’Vj

where Vj is the final velocity of the jet relative to the vehicle, so that (7.9,23) can be rewritten in terms of T instead of m!. The result is

ДCmq=-2CT?-^ (7.9,24)

V j c

For jet airplanes in cruising flight this contribution to Cm is usually negligible. Only at high values of CT, and when the Gm of the rest of the air­plane is small, would it be significant. On the other hand, a rocket booster at lift-off, when the speed is low, has practically zero external aerodynamic damping and the jet damping becomes very important.