Pure Angle of Attack Oscillations

L = 2л pV[28]b

It is now possible to consider the effects of both the circulatory and the noncircu – latory contributions to the unsteady lift. Consider first a pure harmonic variation in a, that is, a = aelwt. Substituting into the expression for the lift given by Eq. 8.13 yields

О

c

Ф

о

it=

Q)

О

О

In terms of the lift coefficient, the result is

Q = = 2n(F + iG) + ink] аеіш. (8.25)

pV2b L J

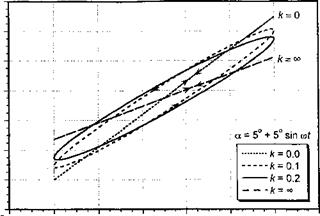
The term inside the square brackets can be considered the lift transfer function, which ac­counts for the difference between the unsteady and quasi-steady airloads. The first term inside the brackets is the circulatory term, and the second term is the apparent mass contri­bution. Notice that the apparent mass contribution is proportional to the reduced frequency and leads the forcing by a phase angle of n/2. If the result is normalized by 2na then

-^ = (F + iG) + i|. (8-26)

2тг|а| 2

The equivalent result for the pitching moment about mid-chord is

|Cm, J.7Г к

№ ~~lT

and where the moment about the 1/4-chord is obtained by a transformation using

Cmi/) = C„m – (8.28)

The results for the unsteady lift are shown in Fig. 8.9, where the significance of the apparent mass contribution to both the amplitude and phase can be appreciated. At lower values of reduced frequency (say, к < 0.1) the noncirculatory or apparent mass forces are small, and the circulatory terms dominate the solution. At higher values of reduced frequency, the apparent mass forces clearly dominate. By setting C(k) = 1, that is, F = 1 and G = 0 in Eq. 8.26, the effects of the shed wake are removed and the quasi-steady result is obtained.[29]