Reynolds number independence

It is interesting to note that the boundary evolution predicted by the Thwaites formula (4.87) with zero initial values at s0 obeys the simple scalings

9(s) ~ [v ~ 1JyjBe, Cy(s) ~ yjv ~ 1 jy/Bk (4.92)

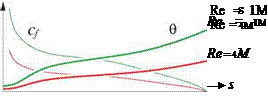
with A(s) and H(s) completely unaffected by the viscosity, or more generally by the Reynolds number. The conclusion is that aside from the simple fBe- scalings, boundary layer evolution and in particular the separation location is independent of Reynolds number, as sketched in Figure 4.24. Only the shape (but not the magnitude) of the input ue(s) distribution matters. This conclusion also holds for effectively exact finite-difference solution methods.

Figure 4.24: For a prescribed ue(s), the resulting shape parameter H(s) distribution of a laminar boundary layer is independent of Reynolds number. The skin friction and momentum thickness distributions arc also unaffected except for simple Cf(s), 9{s) ~ 1 / [Вє – scalings.

However, the assumption that ue(s) is fixed and independent of Reynolds number is not exactly correct for a fixed body geometry. As examined in Chapter 3, the overall potential flow-field and hence ue(s) are affected by the viscous displacement mechanism. The resulting changes to ue(s) themselves scale as 5* ~ 1 / [Вё – and hence are very small, but only if the flow is attached. So in actual applications the Reynolds number independence of laminar flow is only approximately correct, and only in the absence of flow separation.