Sinusoidal Gust: Sears’s Problem

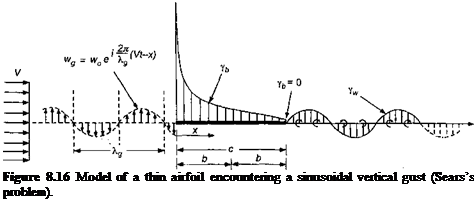
Von Karman & Sears (1938) analyzed the problem of a thin-airfoil moving through a sinusoidal vertical gust field. This is also a frequency domain solution. The gust can be considered as an upwash velocity that is uniformly convected by the free stream, as shown

in Fig. 8.16. The forcing function in this case is

where ajg is the gust frequency. There are two cases of interest. First, if the gust is referenced to the airfoil leading edge then x = 0 and so Eq. 8.38 simply becomes wg(t) = sincogt. Second, if the gust is referenced to the mid-chord, then x = b = c/2 and the forcing becomes wg{t) — cos kg sin aogt — sin kg cos aogt, which is equivalent to a phase shift (see also Question 8.6). The mid-chord was the reference point used in the original work of

von Karman & Sears (1938). In this case, the final result for the lift coefficient can be

written as

Ci = 2 n(^jS(kg)ei2nVIX*, (8.39)

where S(kg) is known as Sears’s function. The gust encounter frequency is given by, 2 nb

kg = — , (8.40)

Ag

where kg is the wavelength of the gust (see Fig. 8.16). Sears’s function can also be computed exactly in terms of Bessel functions and is given by

S(kg) = (J0(kg) — і Ji(kg))C(kg) + iJ{kg) (8.41)

or in terms real and imaginary parts as

mS(kg) = F(kg)J0(kg) + G(kg)Ji(kg), (8.42)

%S(kg) = G(kg)J0(kg) – F(kg)Mkg) + Ji(*g). (8.43)

If the gust is referenced to the leading edge of the airfoil, the result must be transformed, as described previously. This function will be called S’ and can be written as

mS'(kg) = VIS cos kg+%S sin kg, (8.44)

%S'(kg) = — 9^5 sin&g + %S coskg, (8.45)

which is equivalent to a frequency dependent phase shift. The two results are plotted in Fig. 8.17. Notice that the peculiar spiral shape of the S transfer function arises only when the gust front is referenced to the mid-chord of the airfoil. If the gust response is computed relative to the leading edge, then the S’ transfer function is obtained. In application, the gust front reference point is frequently confused in the published literature. While the differences are small at low reduced frequencies, the errors will be significant for kg > 0.2.

The Sears function and the Theodorsen function are compared in Fig. 8.18 in terms of amplitude and phase angle as a function of reduced frequency. At low reduced frequencies the functions converge, but for к > 0.1 the differences become increasingly large. Notice

Figure 8.18 The Theodorsen and Sears functions in terms of amplitude and phase angle as a function of reduced frequency, (a) Amplitude, (b) Phase.

that as к —>• oo then |C(&)| -> 1/2, and the corresponding phase angle -» 0. For Sears’s function, the asymptotic behavior is |S(fcg)| oc l/^/lnkg. When referenced to the mid­chord, then phase angle is proportional to kg — я/4, or —7г/4 if the leading edge of the airfoil is used as the reference point.