SOLUTIONS

In this chapter, three-dimensional small-disturbance solutions will be derived for some simple cases such as the large aspect ratio wing, the slender pointed wing, and the slender cylindrical body. Flow problems requiring more detailed geometries will be treated in the forthcoming chapters.

8.1 FINITE WING: THE LIFTING-LINE MODEL

The three-dimensional lifting wing problem was formulated in Chapter 4, and it is clear that an analytic solution of the integral equations is difficult. However, it is possible to approximate the lifting properties of a wing by a single lifting line, an approximation that will allow a closed-form solution. In spite of the considerable simplifications in this model it captures the basic features of three-dimensional lifting flows, and predicts the reduction of lift slope and the increase in induced drag with decreasing aspect ratio.

8.1.1 Definition of the Problem

Consider a lifting, thin, finite wing (described in Section 4.5) shown in Fig. 8.1, which is moving at a constant speed in an otherwise undisturbed fluid. The free

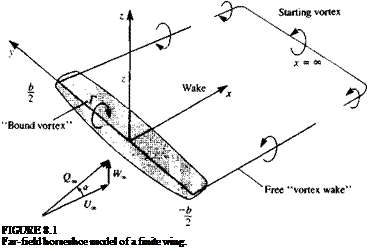stream of speed Qa has a small angle of attack a, relative to the coordinate system which is attached to the wing.

The velocity field for this potential flow problem can be obtained by solving Laplace’s equation for the perturbation potential Ф:

V2<h = 0 (8.1)

Following Section 4.5, the boundary condition requiring no flow across the wing solid surface will be approximated at z = 0, for the case of small angle of attack, by

fWo±).e.(g-„) (8.2)

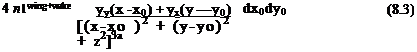where r) = T)c(x, y) is the camber surface (placed near the x, у plane) and for simplicity the subscript c is omitted in this chapter. For modeling the lifting surface, a vortex distribution is selected (as formulated in Section 4.5). The unknown vortex distribution yx(x, y), and yy(x, y) (shown in Fig. 4.9) is placed on the wing’s projected area at the z = 0 plane. The resulting integral equation is

A proper (and unique) solution for the vortex distribution will have to fulfill the Kutta condition along the trailing edge, such that the vorticity component parallel to the trailing edge (yTE.) is zero:

Also, since vortex lines do not begin or end in a fluid (Eq. (4.64)), the solution must comply with

ду*=дУу Эу Bx