Subsonic and Supersonic Flows
In a compressible medium like air, the propagation speed of small perturbations is equal to the speed of pressure waves which in turn is equal to the speed of sound (Shapiro 1953). As the velocity of the moving object gets close to the speed of sound in the air, the effect of compressibility can no longer be neglected. In other words, when the flow velocity is in the same order of magnitude with the propagation speed of the perturbations, we have to consider the compressibility effect. The low flow velocity, compared to propagation speed, enables us to neglect all compressibility effects and identify the flow as incompressible. The measure of compressibility in aerodynamics as a parameter is the Mach number which is defined as the ratio of the flow velocity to the local speed of sound. In this chapter we are going to study the compressible flow, ranging from simple to complex, based on the linear potential theory using point sources and sinks with intensities q related to the perturbation potential. Shown in Fig. 5.1, is the point source, with intensity q, having only radial velocity on the spherical surface whose radius is r.
With the aid of Fig. 5.1 and using the definition of the velocity potential, we can obtain the expressions for the velocity potential in terms of the intensity of the point source as follows.
(i) The relation between the velocity potential ф and the radial and tangential speeds for the steady incompressible flow:
10ф я 0ф • , q
Щ = and Ur = gives ф = —
r oh or 4nr
since in Cartesian coordinates r2 = x2 + y2 + z2 then
U. Gulfat, Fundamentals of Modern Unsteady Aerodynamics, 129
DOI: 10.1007/978-3-642-14761-6_5, © Springer-Verlag Berlin Heidelberg 2010
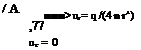 |
||
"il
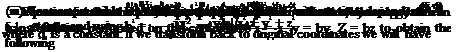 |
(ii) The source expression for incompressible unsteady flow also satisfies the Laplace’s equation with time dependent source strength, q = q(t). The time dependent velocity potential then reads as
(ii) For the compressible unsteady flow we use the full form of 2.24 as follows
02/ і 0 T
![]() 0x2 0y2 0z2 a2 0t 0x
0x2 0y2 0z2 a2 0t 0x
and perform the coordinate transformation of Sect. 2.1.5 in moving coordinates we obtain the classical wave equation
02/ 02/ 02 / 1 02/
ox2+oy2 + oz2=a2 "о?2 (2:26)
The well known solution of the classical wave equation in moving coordinates is
We can go back to original coordinate system in Eq. 5.6 in terms of the free stream speed and the elapsed time t.
Now, let us use the physical models to express the mathematical derivations we have provided in this section.











