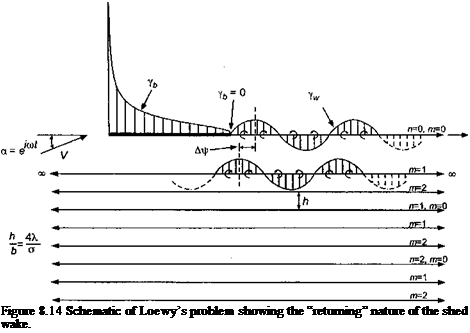
The Returning Wake: Loewy’s Problem

Theodorsen’s theory has represented an isolated 2-D thin-airfoil with the wake convected downstream to infinity. For rotorcraft work, this is perhaps a questionable as­sumption because the rotor blade sections may encounter the wake vorticity from previous blades as well as the returning wake from the blade in question. This fact was acknowledged by Loewy (1957) and by Jones (1958) who set up a model of a 2-D blade section with a returning shed wake, as shown in Fig. 8.14.

This returning wake can be modeled with planar 2-D vortex sheets, just as in Theodorsen’s method, but now with a series of sheets below the airfoil with vertical separation, h, that depend on the mean induced velocity through the rotor disk and the number of rotor blades. Loewy (1957) has shown that in this case the lift on the blade section can be expressed by replacing Theodorsen’s function by

c(k. h) = -______ + _________ , (8.33)

to J Hf(k) + iH^(k) + 2(Ji(k) + iJ0(k))W

where C'(k) is known as the Loewy function, with argument of reduced frequency k. For a single blade, the complex valued W function is given by

w(^—, — ^ = (eM/bei2n(.a>/a) _ jj-i

If a)/ £2 = an integer, then all the shed wake effects are in phase. Notice from Eqs. 8.33 and 8.34 that as h —oo then W■ —► 0 and C'(k) -> C(k), and Loewy’s function approaches

Theodorsen’s result, as it should. For a rotor with Nb blades, the W function is modified to read

W(t’ I’ AVf’ = – l)~’ , (8.35)

where the parameter aj/NbSl now controls the wake phasing.

The wake spacing ratio h/b can be determined from the spacing of the helical vortex sheets that are laid down below the rotor. If an average induced velocity u, = XQR is assumed, then during a single rotor revolution the shed wake generated by a single blade will be at a distance h = (2я/ Q)v, below the rotor. For multiple blades, the spacing will be (27t)Vi/(QNb), that is,

h X£IR2ti AX

b QNbb о with a as the rotor solidity. For = 0, which means that the only phase shift in the wake vorticity results from the spacing between the blades, then

W(~t’ ЇІ’ °’ = (ekh/bei27t(a>/NbQ) – 1) 1 .

Representative results from Loewy’s theory for a one-bladed rotor are shown in Fig. 8.15, where we see that the main consequence of including the shed vorticity below the blade is that it serves to amplify or attenuate the unsteady lift response, depending on the reduced frequency, wake spacing, and wake phase. The most important effects are for lower reduced frequencies, with oscillations at the harmonics of the rotor rotational frequency. Using typical helicopter values of X ^ 0.05 and <7—0.1 gives h/b ^ 2. Therefore, for a helicopter rotor the Loewy function predicts that C’ ~ 0.5 over most of the reduced frequency range, which is an important effect. This can lead to lower damping of blade flapping and flapwise elastic bending modes and will increase the vibratory response of the blade to harmonic airloads. However, it is only for very low advance ratios or for hover that the Loewy effect seems important. Daughaday et al. (1959) have conducted indirect validation of the Loewy effect from measured blade flap bending moments and transient flapping decay data. The reduction in flap damping at frequencies that were multiples of the rotor rotational frequency was verified. Other verifications of the Loewy effect and the implications for rotor aeroelasticity have been made by Ham et al. (1958), Silviera & Brooks (1959), and Anderson & Watts (1975). Hammond & Pierce (1972) have considered a development of the Loewy problem for subsonic compressible flow. Whereas the effects of compressibility are small for со/ £2 near unity, larger differences are noted for co/Q < 1. No equivalent analytic theory to the Loewy problem is available for forward flight; the only option is to solve the problem numerically through discrete vortex wake tracking, a problem discussed in Chapter 10.