THIN AIRFOIL IN GROUND EFFECT

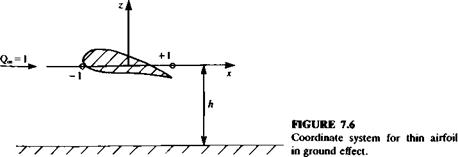
The thin airfoil in ground effect problem will be studied as an example of a perturbation expansion for a case with two small parameters, the standard thin-airfoil parameter (thickness, camber, or angle of attack) and the chord to wall clearance ratio. A thin airfoil is placed in a stream along the x axis (see Fig. 7.6) in the presence of a ground plane located h semichords from the airfoil’s midchord. We will consider a solution linear in thickness, camber, and angle of attack (first-order thin-airfoil theory) for h » 1. It is convenient to use dimensionless variables with lengths scaled by the semichord, speeds by the free stream speed, and the velocity potential by the product of the two. For simplicity, we will drop the bars on the dimensionless variables.

The airfoil boundary condition is transferred to the strip on the x axis with -1 < д: < 1 and the mathematical problem for the perturbation velocity potential becomes

о II О гч >	(7.54)
	(7.55)
ЭФ,
	(7.56)

Equation (7.55) is the airfoil boundary condition from Eqs. (7.10) and (7.13a) and Eq. (7.56) is the ground plane boundary condition. A Kutta condition must be applied at the airfoil trailing edge to complete the problem specification.

The solution is modeled by a distribution of sources of strength a(x) per unit length and vortices of circulation y(x) per unit length along the strip —1 s 1, z = 0 and corresponding image distributions are placed on the strip -1 s* < 1, z = -2A to satisfy Eq. (7.56). The perturbation velocity potential

= 7- f tf(*o){ln i(x – X0f + z2] + In [(x – x0)2 + (z + 2A)2]} dxa 4Jt J_ 1

+ 7- f y(x0)[tan_1 —— tan"1 1 dx0 (7.57)

2^J_i L x-x0 x-Xo-l

To apply the airfoil boundary condition (Eq. (7.55)), we need the limit of the z component of velocity on the singularity strip, which is

x0)2 + 4A2 dX°

+ИгЫ[-^0+(,-17+ л» (7-58)

Compare Eqs. (7.55) and (7.58) and equate the terms that exhibit a jump across the strip to get the source strength

which is seen to be the unbounded fluid result. The remaining terms in the boundary condition then become an integral equation for the unknown circulation density y(x). This integral equation is written

J y(x0)K(x – x„) dx0 = —21 (х0)Л(х — x0) dx0 + 2л(^а — ~j~j (7-60)

H(x) – 2 ^ 2

v ’ x2 + 4h2

1

x x2 + 4A2

To solve the integral equation we use an approach due to Keldysh and Lavrentiev (see Plotkin and Kennell7 3 for details) and seek an expansion in 1/A of the following form:

The expansion coefficients are found to be

Hm = (—l)1+m/2 2_(m+1) (7.62a)

Kn = (—1)("+1)/2 2-("+1) (7.626)

when m is even and n is odd and are zero otherwise. Equations (7.61) are substituted into the integral equation (Eq. (7.60)) and terms with like powers of 1/6 are collected. The following system of thin-airfoil-like equations for the unknown yn{x) is obtained:

f ^^-dx0=- 2І H^^J1 (xa){x – x0)n~l dx0 J-iX—Xq J_ і ax

rl n — 1

– 2 Km(x-Xo)mYn-m-i{x0)dx0=fn(x) (7.636)

j-l m= 0

The solution to Eqs. (7.63) that satisfies the Kutta condition is obtained with the help of Eq. (7.19) as

For n = 0, the unbounded fluid result is recovered

Let us find the first term in the expansions for the thickness, camber, and angle of attack problems separately. Note that each expansion has either all odd or all even terms so that the terms we neglect are two orders smaller than the ones we keep. Since the thickness and camber problems require the choice of a particular airfoil to proceed, let us begin with the angle of attack problem.

The expansion for the circulation density has terms for n = 0, 2, 4,. . . and for n = 2 the function on the right-hand side of the integral equation (Eq. (7.636)) is

f2 = -2K1a{ J^—^(x-x0)dx0 1 + x0

(l-*o)(*-*o) ла 1ч Vi-4 +

_a j 1-х f1 11 +x0x0+l/2 а /Г

2л Vl +x J_! VI – x0 x0-x 0 2V1

(Note that

Ґ jl+Xof (x0) J г1 1+ДСо /Ы,

J_,*■

is introduced so that the integrals in Appendix A can be used).

As an example to illustrate the camber effect, choose the parabolic arc camberline given by

r,, = P( 1-х2)

The expansion for the circulation density has terms for n = 0, 2, 4,… and the unbounded fluid result (n = 0) is found from Eq. (7.65) as

УоСО = – — f *oЛїї–*0 dX°- = 4/3Vl—*2 (7.68)

л Vl+xJ-j VI-XqX-Xo

For n = 2, the function on the right-hand side of the integral equation (Eq. (7.636)) is

/2 = 0* J (*-*o)Vl-Xodio = – p (7.69)

and the solution for the circulation density for n = 2 is found from Eq. (7.64) as

*0 dx0 – p

X0X0-X 2

As an example to illustrate the thickness effect, consider the approximate Joukowski airfoil with thickness function given by

= Ti(l — *)Vl – x2

The expansion for the circulation density has terms for n = 3, 5,… and for n = 3 the function on the right-hand side of the integral equation (Eq. (7.636)) is

r _ г j f1 (2xl ~ *0 “ 1)(* – xQ)2 ‘■"ТІ, — 4

-і——- *.= – y(< + J) (7.71)

and the solution for the circulation density for n = 3 is found from Eq. (7.64)

ті /і – x f1 , 1. /і + Xo dx0 t, / 1-х , ,

Vr^ J_, +—j Vttj+» <772>

The lift coefficient for the airfoil is found from the nondimensional circulation density as

The lift coefficients for the separate angle of attack, camber, and thickness effects which include the first term in the ground-effect expansion are obtained by substituting Eqs. (7.67), (7.70), and (7.72) into Eq. (7.73) to get

Angle of attack:
С, = 2ла[ + th~2 + 0(/t~4)]	(7.74a)
Parabolic arc camber:
Ci = 7T/S[1 -h~2+ 0(A~4)]	(7.746)
Joukowski (thickness):
Q=_l6 h~3 + 0{~h~5)	(7.74c)

Note that the first term in Eq. (7.74a) is identical to the result obtained in Section 5.5 using a single-element lumped-vortex model (in Eq. (7.74a) remember that h is normalized by the semichord). Additional terms for the angle of attack and Joukowski solutions may be found in Plotkin and Kennell.73 It is seen that for these examples and for the assumptions connected with the expansions the ground plane increases the lift due to angle of attack and causes a decrease in lift due to the airfoil thickness and camber.