White’s equilibrium method

The Thwaites method’s functions Fq(a), T(a), and H(A) are valid only for laminar flow. To integrate the von Karman momentum equation (4.28) for a turbulent boundary layer, it is necessary to provide turbulent closure relations for Cf and H, ultimately in terms of the primary unknown в and the inputs v and ue. Such an approach is described by White [22], mainly for illustrative purposes. It is summarized below.

A suitable turbulent skin-friction relation is the Coles formula, which is a fit to equilibrium flow data.

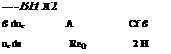A suitable turbulent shape parameter relation is the G-beta locus (4.58), after replacement of G and в by their definitions (4.56), (4.57). Squaring both sides and further multiplying through by Cf /2A2 gives the more convenient form

where Л is a new pressure-gradient parameter. This is a scaled version of Thwaites’s A, and is more relevant for turbulent flows.

Equations (4.93) and (4.94) are two constraints between the four parameters H, Cf, Л, Re#. If Л and Re# are specified, these equations can be numerically solved (e. g. by Newton iteration) for the corresponding H and Cf values. Hence, we in effect have

which are the direct replacements of Thwaites’s T(a) and H(a) closure functions.

We can now insert the Cf and H functions (4.96) into the von Karman equation (4.28), putting it into the following functional form.

^ = ^ef(A, Bee) – (й(А,&в) + 2^ Л = f(e, ue, v) (4.97)

If v and ue(s) are provided, then this can be numerically integrated for the в(«) distribution, usually starting from the transition location str. The initial value e(str) is also required, and typically would be obtained from the last laminar в value at str.

In contrast to the laminar boundary layer Reynolds number independence discussed earlier, turbulent bound­ary layer evolution is affected by Reynolds number. This can be seen from the explicit appearance of the Reynolds number in the H(Л, Взв) function (4.96). In general, increasing Re# tends to decrease H slightly, giving slightly greater resistance to adverse pressure gradients. Consequently, increasing the overall Reynolds number of a turbulent flow tends to delay separation and increase maximum lift.