A SKEWED Ц LOWER BOUND
Like the exact value of p, the exact value of v can be obtained as the global maximum of a non convex optimization problem. In the spirit of (Packard et al., 1988; Young and Doyle, 1990), a power algorithm is proposed for solving this problem. The necessary conditions of optimality are rewritten as x = f(x), and a lower bound of и corresponds to a limit of the sequence x^+i = /(a;*). Even if the sequence does not necessarily converge and if the result depends on the initial value xo, this algorithm usually exhibits good convergence properties and a low computational burden.
The optimization problem is first introduced in Proposition 3..1, which is an extension of Proposition 6.2.c of (Fan and Tits, 1992). The power algorithm is then proposed in propositions 3..2 (see appendix B for the proof) and 3..3.
PROPOSITION 3..1
![]() v{M) – maxpr(QM — Р,Рї)
v{M) – maxpr(QM — Р,Рї)
where (A = diag(Aі, Д2) and mi is the dimension of Ai):
pr(A, B) = sup(|A| / det(A — XB) = 0 and A Є R) (8.23)
Q = {A / 6ІЄ [-1,1], SfSI = 1 and A°HAC = 1} (8.24)
pr(A, B) is called the generalized spectral radius of matrices A and B. The rest of the exposition is simplified by considering a block structure with just a real repeated scalar, a complex repeated scalar and a full complex block. The general case of a mixed uncertainty is easily obtained by duplicating the appropriate formulae for each block.
PROPOSITION 3..2 Let A = diag(6[Ikl, 6flk2, A^)vith А? Є Скз’кзА
lower bound P of v(M) must satisfy:
|
M*z – (3w |
 |
||
(8.25)
![]()
![]() a*2w 2 a3
a*2w 2 a3
bi = qai, b2 = j-;—ra2, 63 = ,—r а^гі to3
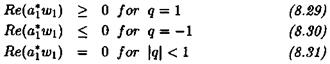 |
for some real scalar q Є [—1,1] with:
 |
|.| denotes the Euclidean norm. The complex vectors b, a, z and w are partitioned compatibly with the uncertainty structure as:
with e. g. bi Є Cki.
Remark: the above Proposition is an extension of Theorem 4 of (Young and Doyle, 1990). It is applicable under technical non-degeneracy conditions exposed in this reference.
A solution to this system of equations can be found via a power iteration method.
PROPOSITION 3..3 Consider the following power iteration:
– w2 ,ka2,k + l |u>3,fc|
zi, k+i = qk+iwi’k, z-2,k+i = і—;—————– ;W2,k, Z3,k+i = і———– гОзл+і
w2ka2,k+i |оз,*.+і|
|
+ Re{a*i, k+lwi, k) |
![]()
Pk+lWk+l = ^ ^q1 і ^ M*Zk+
iff 1 > f I > 1 f then qk+f > ff else qk+i = otk+i.
![]() 14*1
14*1
lal, fc+ll
iff >> 1 I > 1 i then >> 1 > ff else qk+i = аш.
and(3k+i, j3k+i are chosen positive real so that |afc+i| = wk+\ = 1.
If the algorithm converges to some equilibrium point, then тахфф) is a lower bound for u{M).
Remarks:
(/’) An alternative to equation (8.33) is to use a first order filter 7*;+i = xjк + (1 — х)тахфкфк) where x = e~l/N. If necessary, a large value of N can be chosen to recover the convergence properties of the standard power algorithm of (Young and Doyle, 1990).
(ii) The power algorithms of (Packard et al., 1988; Young and Doyle,
1990) usually exhibit good convergence properties and a low computational burden. Nevertheless, when considering complex model perturbations, "limit-cycles can occur, and seem to occur more often when there are large repeated scalar blocks" (Packard et al., 1988). In the same way, "significantly poorer convergence properties" are obtained in the case of a real model perturbation (Young and Doyle, 1990). In this last case, note that the extension to skewed ц problems of the method of chapter 5 (section 3.) is essentially straightforward.











