AN AUGMENTED p PROBLEM

• As a preliminary, using equation (8.6), it is first easy to prove that:

Ff1/4(D1Fl(M, A2)D];1 – = Ft(H, A2) (8.14)

with:

‘ #n #12 ‘ #21 #22 .

Ff1/4DiM12

M2lD^Ffl/4

M22

Note especially that H22 = M22 • Lemma 2..4, which is inspired by a previous work in (Sideris and Pena, 1990), transforms the original skewed p problem into an augmented p problem (see appendix B for the proof).

LEMMA 2..4 Let:

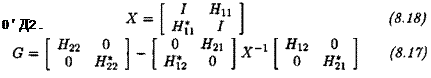(8.16)

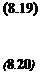Assume that ст(#ц) < 1 and let к < 1//ід2(#2г)- Then: а(ЩН, А2)) < 1 УД2 Є kBA2

if and only if:

det(I – AG) ф 0 MA2 Є kBA2

Remarks:

(i) Matrix X is invertible in the above Proposition because of the as­sumption <x(#n) < I-

(ii) Lemmas 2..1, 2..2 and 2..3 do not require the assumption of a real
diagonal model perturbation Д2. This one is however necessary in the above Lemma.

• The mixed и upper bound is presented in the following proposition. Its proof is a straightforward application of Lemmas 2..3 and 2..4.

PROPOSITION 2..5 Let M a complex matrix. Let Dgnd Gsome (D, G) scaling matrices associated to the model perturbation A. Let F = I + G and H the complex matrix of equation (8.15). Let ma(G) the s. s.v. of equations (8.16) and (8.17). Assume that Мд(£) > ^Д2№г) and< Hi < ) < 1 . Then << ( G) is an upper bound of v(M).

Remarks:

(i) The following subsection presents simple methods for computing scal­ing matrices D and Gi.

(ii) For fixed values of scaling matrices D and G, the simplest solu­tion for obtaining a и upper bound with Proposition 2..5 is to compute an upper bound of p^(G), typically the mixed p upper bound of (Fan et al., 1991). Since this one is directly available in the < Analysis and Synthesis Toolbox or in the LMI Control Toolbox, the implementation of a computational algorithm is rather easy.

(Hi) Nevertheless, a technical difficulty is to check the condition p^(G) > Pa? (-/VT22)і when p bounds are computed instead of the exact values. A solution is to check that pLB&(G) > puв, д2(ЛТ22), where рів and рив mean p lower and upper bounds.