Group Velocity and Dispersion

Note that by Eq. (4.8), for large t,

. da

a + [x — m (a)t—– > a

. da

—m + [x — m (a)t- > —m,

dt

where m'(a) = (dm/da). Thus, locally, вx and —вt (subscript denotes partial deriva­tive) may be taken as the wave number and angular frequency as t ^ to. To find the phase velocity, one may keep в constant in Eq. (4.8) and differentiate with respect to t to obtain

r da dx

[x — m (a)t ——+ a— m = 0.

d t dt

For large t, by the above equation, the phase velocity is found to be

Now the asymptotic solution (4.6)-(4.9) may be given the following interpretation.

1. Each Fourier component with wave number a is constant along a ray in the x-t plane and propagates with group velocity m'(a) as shown in Figure 4.1. This is because x = m'(a) t so that a is a constant along a given line (ray) x/t = constant.

Figure 4.1. (a) Rays of x = K(a)t for constant a in the x-t diagram. (b) Ini­tial energy spectrum.

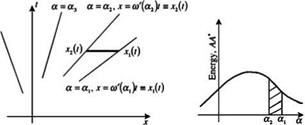Furthermore, dx/dt = K(a), suggesting that K(a), the group velocity, is the speed of propagation of wave number a.

2. Far away, the waves may be regarded as initiated locally near x = 0. After a period of time, the waves spread out in space because a different Fourier component with different wave number a propagates with different speed (O(a) = 0), see Figure 4.1a.

A quantity of interest in wave propagation is the wave energy that is A2 = AA* (* denotes the complex conjugate). The wave energy, Q(t), between two rays x = x1(t) = o'(a1) t and x = x2(t) = K(a2) t (see Figure 4.1a) is

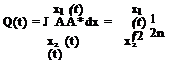With t fixed, a change of integration variable from x to a gives

dx = t O’ (a)da.

Hence,

H(a, K) dD do

Q(t)

Therefore, energy is constant between group lines. In other words, the wave energy of the initial energy spectrum (Figure 4.1b) propagates with group velocity. The group lines diverge with a separation that increases with t. Hence, the wave amplitude A decreases as t-(1/2).

It is important to point out that this analysis clearly shows that propagation speed and dispersion have nothing to do with phase velocity. Dispersion arises because of the variation of group velocity with wave number. For a more detailed treatment of dispersive waves, a reading of the book by Whitham (1974) is highly recommended.