Incompressible Flow Theory
The prediction of unsteady lift, airfoil pitching moment and the hinge moment on an airfoil for a harmonic flap oscillation in incompressible flow has been studied by Kiissner & Schwartz (1941), Theodorsen (1935), and Theodorsen & Garrick (1942) by means of unsteady thin airfoil theory. The results are known exactly for the frequency domain and can be reformulated in the time-domain with arbitrary flap motion using Duhamel superposition. Other contributions have been made by Drescher (1952). As shown previously for an incompressible flow, the unsteady lift and moment coefficients on a thin airfoil
2V2
The first term in each of the above equations is the noncirculatory (apparent mass) component. The second group of terms in the equations are all circulatory components, with the Theodorsen function C(k) accounting for the influence of the shed wake vorticity.
With the addition of a trailing edge flap hinged at eb (measured from the mid-chord) there are additional airloads produced that depend on the flap deflection angle, <5, and its time rate-of-change, S – see Fig. 8.41. These additional terms are
 dbfdt
dbfdt
Perturbation velocity to flap deflection rate, db/dt
Figure 8.41 Nomenclature for airfoil with a trailing edge flap. Perturbation velocities are produced by trailing edge motion: (a) flap displacement, (b) angular rate about the hinge.
where, again, the first group of terms in each equation are of noncirculatory origin. The addition of the trailing edge flap also gives rise to a hinge moment, which is

Cfi = – A- (2FBb2a – Fbfi) – AC(k)
and
where the individual contributions to the hinge moment in response to the airfoil motion and in response to the flap have been written out explicitly. In the above equations, the “F” terms are geometric constants that depend only on the size of the flap relative to the airfoil chord and are listed by Theodorsen (1935) and by Hariharan & Leishman (1996).
Because of the linear assumption in the thin-airfoil theory, the loading contributions from the airfoil and from the flap can be obtained by superposition. Therefore, the lift, pitching moment and hinge moment in response to independent oscillatory airfoil motion and oscillatory flap motion can be written in coefficient form as
Cn(t) = Cnnc{t) + 2nC(k)(aqs + 8qs), (8.207)
and
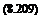
![]() /г.»
/г.»
Ck(t) = Cf (r) + -^-C(k)(aqs + V) + Cf (f),
where
„„ nba b r .. . .. 1
Cn (0 — —Q—I" [nfl ~ nbaa – VF48- bFx8] ,
c"'(0 = ІЇІ + a2) a – abh] – A. [F, + (e _ a)F,] ЬЧ. (8.211)
C**(0 = -Ар ЬгV (I – a) ba + (F4 + Ft0) V4
|
|
|
|
|
|
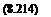 + – v2 (F, – f4f, o) a – f VbSF4Ft
+ – v2 (F, – f4f, o) a – f VbSF4Ft
7T 2 JT
Notice that in these foregoing expressions several terms have been grouped together; aqs is the quasi-steady airfoil AoA and 8qs is the quasi-steady AoA in response to the imposed flap motion as given by
The foregoing equations hold good only for oscillatory motion of the airfoil and/or the flap. However as shown previously the results can be transformed to handle arbitrary motion by means of Duhamel’s superposition integral with the Wagner indicial (step) response. In the time domain, the unsteady aerodynamic loads can be written as
where фу/ is the Wagner function. This can be written approximately using an exponential function, as shown in Section 8.10. Using these results state-space equivalent arbitrary
Cl(t) = г-ж [(М2/2)(£)2 (А, Ь, + А2Ьг)(і)] [zl((>] + (8’219)
= я (a + 1) [(ЬіЬа/2) (^f (A,6, + A2b2) (f)]
![]()
![]() +їИ)
+їИ)
where
Notice that the coefficient terms in the foregoing equations for the flap are the same as for the AoA terms. This is because the circulatory lag function itself [i. e., C(k) or фу/] does not depend on the mode of forcing for incompressible flow (i. e., it does not depend on a, a, 8, or <$). Furthermore, the noncirculatory components and the contributions in response to the quasi-steady terms of the lift, pitching moment and the hinge moment are proportional to the instantaneous displacements for an incompressible flow and involve no additional states. They can be computed directly using Eqs. 8.210-8.214. The circulatory lift acts at the aerodynamic center but there are no additional states required to calculate the pitching moment. Therefore, the complete aerodynamic system for the airfoil and flap in an incompressible flow can be represented by a set of four aerodynamic states. Although it is convenient to separate out the circulatory lift in response to airfoil motion from that in response to the flap motion, in a practical application their net effects can be combined so that, in fact, only two states are required to compute the net circulatory airloads.











