Inviscid Theories of Hypersonic Flows

12.2.1 Hypersonic Potential Flow

In 1946, Tsien [41] derived similarity laws of hypersonic flows, following von Kar – man analysis of transonic similitude. Assuming isentropic, irrotational flow, Tsien used the full nonlinear potential equation with the tangency boundary condition at the solid surface (and not the linearized boundary condition). In the case of two – dimensions, let

dp dp

u = U + , v =

dx dy

The governing equation for the perturbation potential is

u2 d2p uv d2p v2 d2p

a2 dx2 + a2 dx dy + a2 dy2 ^

where

a2 = a2 – 1-1 ((u2 + v2) – U2)

a0 is the undisturbed speed of sound at flow velocity U.

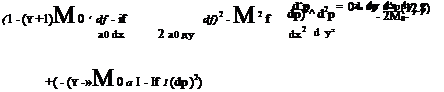For hypersonic flow, a0 and dp/dx, p/dy are small compared to U, hence retain­ing terms up to second order, the equation for p becomes

Tsien [41] introduced the coordinate transformation

x y

С —, n =~ (12.9)

c e

where c is the chord and e is the thickness of the airfoil. He justified this choice since for hypersonic flow over a slender body, the variation of fluid velocity due to the presence of the body is limited to a narrow region close to the body.

The corresponding non-dimensional form for y is

a0 c

The lift curves are parabolas and as K ^to, Cl ^ (y + 1)a2.

For M0 < 3, Ackeret theory gives reasonable results where Cl = 4a fj M2 – 1, and the lift curve is a straight line.

For profiles with thickness, Linnell reported the results for diamond airfoils at angle of attack.

For hypersonic flow, the pressure change across a shock of given turning angle is much greater the across an expansion wave of equal turning angle. To avoid a leading edge shock, it is desirable to operate with large angles of attack. Since most of the lift is furnished by the lower surface, it follows that expansion on the lower surface is undesirable and the best profiles have flat lower surfaces.