Kernel Function Method for Subsonic Flows

The Kernel function method, known also as the pressure mode method, is used for solving the lifting pressure value via the integral equation, 5.37, for the prescribed motion of a thin wing in subsonic flows. The expression for the Kernel function was given in Eq. 5.36 as follows.

Oz2 Oz R

—1

Watkins et al. gives the open form of the kernel function in terms of the hypergeometric functions; K1: first order modified Bessel function of the second kind, If. first order modified Bessel function of first kind, and L1: first order modified Struve function as follows.

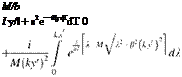Mkx +^J(kx’)2+b2(ky’)2 ф ukX+^J(kx )2+b2(ky’)2]

(Mky f J(kx )1+b’2(ky )2

(5.42)

Here, all the coordinates are nondimensionalized with root half chord, b0.

In order to solve for the lifting pressure with the kernel function method we need to expand the lifting pressure in to the sin series similar to that given for Eq. 5.40. In doing so, we need to transform the chordwise coordinates for an arbitrarily shaped planform as shown in Fig. 5.4.

As seen in Fig. 5.4, at any station along span, we use an angular coordinate в along the chord. The midchord variation along the span can be expressed in terms of the spanwise coordinate g. Using this approach we can deal with the planforms having not only straight but also curved edges. Now, we can write the chordwise H coordinate in terms of the angular в coordinate as shown in Fig. 5.4 as follows

The unknown lifting pressure in Eq. 5.37 can be expressed in terms of the transformed coordinates in a following manner.

Dp (в, g)= 4 ppU2 Ь(в, g) b0

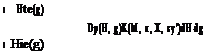Substituting 5.43 into 5.37 gives

Now, we can expand the nondimensional lifting pressure, Ь(в, g), into proper series (Ashley et al. 1965) as follows

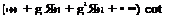L(в, g)=-bv1 – g2

+ (яю + g Я11 + g2«12 + –•) sin в…

42 +22^(ял0 + g Яп1 + g яп2 + • — sin пв

Here, coefficients япт are the unknowns to be determined. Equation 5.45 can be written as the product of two entities as follows

ь(в, g)=у X inmn(g) (5.46)

п

In 5.46, for n = 0: 10(в) = cot |, and Іп(в) = ^ sin пв, n > 1,

An (g) = J 1 – g2 (Яп0 + gЯп1 Л———— h gm«nm Л—- ) = V1 – g2 X gm«nm

т

(5.47)

If there is a symmetric loading on the wing we take the even powered terms and for the antisymmetric loading the odd powered terms of series 5.47.

The integral equation 5.44 has a kernel with a strong singularity. In order to prevent the difficulties in numerical integration function K is rewritten as K with a scaling presented in a following manner

K[M, k, x’, s(y – g) = bls2(y – g)2K[M, k, x’, s(y – g), s = l/bo The integral equation with the aid of 5.48 becomes

Here, in its open form K reads as

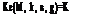M, k, X – Пт + Ъ cos в, s(y – g)

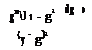The series expressions 5.46-5.47 for the nondimensional lifting pressure, L(h, g), can be substituted in integral equation, 5.49, to obtain the following system of linear equations written in double series

The right hand side of the Eq. 5.50 is given as the boundary condition. Unknown coefficients, anm, at the right hand side of the equation can be deter­mined with taking as many control points on the wing as unknowns. The lifting pressure values at these stations are then calculated using 5.46.

In Fig. 5.5, there are 20 (5 spanwise x 4 chordwise) unequally spaced control points, including the root chord, on a symmetric wing. There are some rules to follow while choosing the control points. These are:

(i) No control points are placed at the wing edges. Sufficient number of points, no less than 20, in chordwise and spanwise directions must be taken.

(ii) In symmetrical loadings even powers of m and antisymmetrical loadings odd powers of m must be considered.

(iii) For high reduced frequencies more number of control points must be taken.

(iv) If there are control surfaces on the wing the control points must be chose accordingly.

Hitherto, we have formulated the kernel function method applicable to subsonic flows over thin wings. In next section we are going to study a new method called

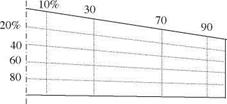Fig. 5.5 Representative con­trol points on the wing

‘Doublet-Lattice’ method applicable to general problems involving more complex wings with control surfaces and tails and tail wings.