Limitations of Rigid Body Model

The 6DOF model in Equations 3.44, 3.46, 3.47, and 3.50 involving the rigid body states is generally adequate to predict rotorcraft dynamics in low – and mid-frequency range. In the conventional rigid body model, the main rotor dynamics are omitted and the rotor influence is absorbed by the rigid body derivatives. A better prediction at higher frequencies, however, necessitates the inclusion of rotor dynamics in the estimation model. One approach to include rotor effects in a 6DOF model is introdu­cing equivalent time delays in control inputs [11,12]. These delays can be determined by correlating model response with flight data. This is, however, an inappropriate alternative to modeling the rotor dynamics, which are highly complex in nature. Model inversion is required for the feed forward controller in the design of a model following control systems and the time delays become time lead on inversion, which means that the future values of the state variables are needed in advance. This is unrealistic for an online real time process like in-flight simulation. It clearly underlines the need to develop extended models with an explicit representation of rotor dynamic effects. Therefore, the 6DOF rigid body model is generally extended with additional degrees of freedom representing the longitudinal and lateral rotor flapping.

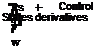The basic approach to extend the 6DOF rigid body model is shown in Figure 3.16. The model structure now includes two additional degrees of freedom

representing the longitudinal and lateral flapping [10,11]. The state-space matrix in Figure 3.16 defines the submatrices pertaining to rigid body, rotor, and the cross-coupling matrices for body-to-rotor and rotor-to-body. In a simplified rotor model, the longitudinal and lateral flapping angles can be expressed primarily as a function of body angular rates and control inputs. In Ref. [12], Kaletka et al. formulated an 8DOF extended model by redefining the roll and pitch acceler­ations for rotor/body motion and using them as state variables. Tischler provided a hybrid body/flapping model, which coupled the simplified fuselage equations at low frequencies to the simplified rotor equations at high frequencies with equiva­lent spring terms [13]. The following first-order coupled differential equations for longitudinal flapping a1s and lateral flapping b1s can be appended to the 6DOF model:

a 1s = A; b 1s = B (3.51)

Here, A and B are the longitudinal and lateral flapping-specific moments.

EPILOGUE

An extensive treatment of EOMs is found in one of the earliest books [1]. Extensive helicopter research work on aeromechanics is reported in Ref. [14]. It takes a systems approach and deals with three major aspects of helicopter research, which are also equally applicable and suitable to fixed wing aircraft research and development: (1) reality and conceptual model linking through wind tunnel simulation—this is analysis route (Appendix A, Chapter 4), (2) linking of conceptual model (Chapters 3 and 5) and computerized model via model verification—this is the programming route, and (3) linking of computerized model and back to the reality via system identification/model validation procedure—this is the computer simulation route (Chapters 6 and 9).